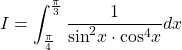Đặt ẩn phụ giải tích phân lượng giác
Các bài toán tính tích phân lượng giác thường được giải bằng phương pháp đặt ẩn phụ nếu như không giải được bằng các nguyên hàm lượng giác.
Đặt ẩn phụ là phương án thường nghĩ tới khi giải phương trình, bất phương trình. Và nó cũng sử dụng để giải các tích phân của hàm lượng giác.
Phương pháp đặt ẩn phụ giải tích phân lượng giác
Tích phân hàm số lượng giác có dạng tổng quát:
![]()
Tùy thuộc vào tính chất và dạng đặc biệt của hàm ![]() hoăc mối quan hệ giữa hàm
hoăc mối quan hệ giữa hàm ![]()
![]()
![]()
Dạng số 1: Nếu hàm lượng giác chẵn với Sin và Cos
Tức là: ![]()
![]()
![]() là hàm số chẵn theo
là hàm số chẵn theo ![]() và
và ![]() )
)
Cách giải: Đặt ![]() hoăc
hoăc ![]()
Bài toán 1. Tính tích phân
![Rendered by QuickLaTeX.com \displaystyle I=\int_{{\frac{\pi }{6}}}^{{\frac{\pi }{3}}}{{\frac{{\sqrt[3]{{{{{\sin }}^{3}}x-\sin x}}}}{{{{{\sin }}^{3}}x}}}}\cot xdx](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-a2d2f48e0fe8787d5aff0af78034aef6_l3.png)
Giải:
Rõ ràng ![]() nên nó là hàm số chẵn theo
nên nó là hàm số chẵn theo ![]() và
và ![]() .
.
Ta có:
![Rendered by QuickLaTeX.com \displaystyle I=\int_{{\frac{\pi }{6}}}^{{\frac{\pi }{3}}}{{\frac{{\sqrt[3]{{1-\frac{1}{{{{{\sin }}^{2}}x}}}}}}{{{{{\sin }}^{2}}x}}}}\cot xdx=\int_{{\frac{\pi }{6}}}^{{\frac{\pi }{3}}}{{\frac{{\sqrt[3]{{1-\left( {1+{{{\cot }}^{2}}x} \right)}}}}{{{{{\sin }}^{2}}x}}}}\cot xdx=-\int_{{\frac{\pi }{6}}}^{{\frac{\pi }{3}}}{{\frac{{\sqrt[3]{{{{{\cot }}^{2}}x}}}}{{{{{\sin }}^{2}}x}}}}\cot xdx](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-725a4e71525fe64de5dd448bc88b75ea_l3.png)
Đặt ![]()
Khi ![]()
Từ đó
![Rendered by QuickLaTeX.com \displaystyle I=\int_{\sqrt{3}}^{\frac{1}{\sqrt{3}}} t^{\frac{1}{3}} \cdot t d t=\int_{\sqrt{3}}^{\frac{1}{\sqrt{3}}} t^{\frac{5}{3}} d t=\sqrt{\frac{1}{8}\left(9 \sqrt[3]{3}-\frac{1}{\sqrt[3]{3}}\right)}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-35d0703ed49d2416b70be4fc063ba917_l3.png)
Dạng số 2: Nếu hàm số lượng giác lẻ với Cos
Tức là: ![]() (
(![]() là hàm số lẻ theo
là hàm số lẻ theo ![]() )
)
Cách giải: Đặt ![]()
Bài toán 2. Tính tích phân
![]()
Giải:
Ta thấy ![]() nên
nên ![]() là hàm số lẻ theo
là hàm số lẻ theo ![]()
Ta có
![]()
Đặt ![]()
Khi ![]()
Từ đó:
![]()
Dạng số 3:Nếu hàm số lượng giác lẻ với Sin
Tức là: ![]() (
(![]() là hàm số lẻ theo
là hàm số lẻ theo ![]() )
)
Cách giải: Đặt ![]()
Bài toán 3. Tính tích phân
![]()
Giải:
Ta thấy ![]() nén
nén ![]() là hàm số lẻ theo
là hàm số lẻ theo ![]()
Đặt ![]()
Khi ![]()
Ta có:
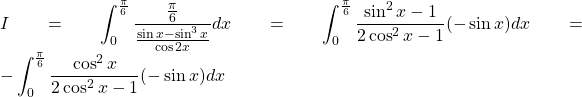
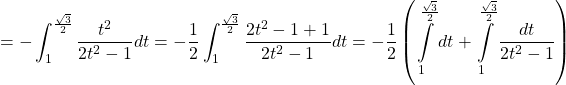
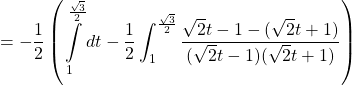
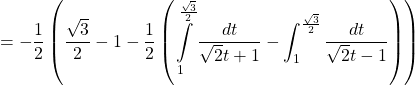
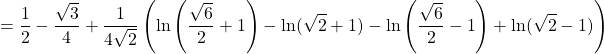
Dạng số 4: Nếu hàm số lượng giác dạng phân thức
Tức là: ![]()
Cách giải: Đặt ![]()
Bài toán 4. Tính tích phân ![]()
Giải:
Đặt 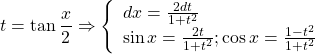
Khi ![]()
Ta có
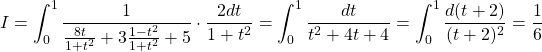
Bài toán 5. Tính tích phân
![]()
Trong đó n là số nguyên dương
Lời giải:
Đặt ![]()
Khi ![]()
Từ đó
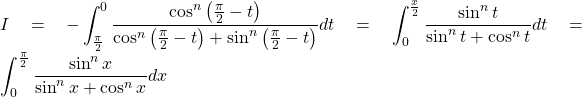
Do đó
![]()
Vậy ![]()
Bài toán 6. Tính tích phân
![]()
Lời giải:
Ta có
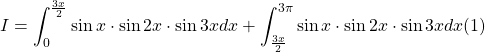
Xét tích phân
![]()
Đặt ![]()
Khi ![]()
Từ đó
![]()
![]()
Từ (1) và (2) ta được ![]() .
.
Bài tập tích phân lượng giác
Tính các tích phân lượng giác sau:
1. ![]()
2. ![]()
3. ![Rendered by QuickLaTeX.com \displaystyle I=\int_{{\frac{\pi }{6}}}^{{\frac{\pi }{3}}}{{\frac{1}{{\sqrt[4]{{{{{\sin }}^{3}}x\cdot {{{\cos }}^{5}}x}}}}}}dx](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-911a060c3f92985a1dd0279747769cad_l3.png)
4. 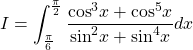
5.