Cách chứng minh 3 điểm thẳng hàng bằng vectơ
Lên lớp 10 các em được học các quy tắc về vectơ, và vectơ tỏ ra khá hữu dụng để chứng minh 3 điểm thẳng hàng.
Ba điểm thẳng hàng là 3 điểm cùng nằm trên một đường thẳng.
Trong vectơ, 3 điểm ![]() thẳng hàng ⇔
thẳng hàng ⇔ ![]()
![]()
![]()
![]()
![]()
![]()
Sử dụng vectơ chứng minh 3 điểm thẳng hàng
Chứng minh: ![]()
![]()
![]()
![]()
![]()
![]()
– Sử dụng các quy tắc biến đổi vectơ đã biết.
– Xác định vectơ ![]() và
và ![]() thông qua các tổ hợp trung gian.
thông qua các tổ hợp trung gian.
* Chú ý:
– Cho ba điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
– ![]()
Với điểm ![]() tùy ý và số thực
tùy ý và số thực ![]() bất kì.
bất kì.
Đặc biệt khi ![]() thì
thì ![]() thuộc đoạn
thuộc đoạn ![]() .
.
Ứng dụng vectơ chứng minh 3 điểm thẳng hàng
Bài toán 1: Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường chéo AC thỏa mãn tỉ số ![]() . Chứng minh ba điểm D, E, I thẳng hàng.
. Chứng minh ba điểm D, E, I thẳng hàng.
Giải
Ta có: ![]()
![]()
![]() (1)
(1)
![]()
Theo giả thiết, ta suy ra:
![]()
![]()
![]()
Từ đây ta có:
![]()
![]()
![]()
![]()
![]() (2)
(2)
Từ (1) và (2) suy ra: ![]()
Vậy ba điểm D, E, I thẳng hàng.
Bài toán 2: Cho ![]() ABC. Gọi O, G, H theo thứ tự là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm của
ABC. Gọi O, G, H theo thứ tự là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm của ![]() ABC. CMR O, G, H thẳng hàng.
ABC. CMR O, G, H thẳng hàng.
Giải
Ta có:
![]() (1)
(1)
Gọi E là trung điểm BC và ![]() là điểm đối xứng với A qua O, ta được:
là điểm đối xứng với A qua O, ta được:
![]()
![]() là hình bình hành
là hình bình hành
![]() , E, H thẳng hàng
, E, H thẳng hàng ![]()
![]()
Ta có:
![]() (2)
(2)
Từ (1) và (2) suy ra:
![]() thẳng hàng.
thẳng hàng.
Bài toán 3: Cho ba dây cung song song ![]() của đường tròn (O). Chứng minh rằng trực tâm của ba tam giác
của đường tròn (O). Chứng minh rằng trực tâm của ba tam giác ![]() nằm trên một đường thẳng.
nằm trên một đường thẳng.
Giải
Gọi ![]() lần lượt là trực tâm của các tam giác
lần lượt là trực tâm của các tam giác ![]()
Ta có:
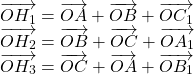
Suy ra:
![]()
![]()
![]()
![]()
Vì các dây cung ![]() song song với nhau
song song với nhau
Nên ba vectơ ![]() có cùng phương
có cùng phương
Do đó hai vectơ ![]() cùng phương hay ba điểm
cùng phương hay ba điểm ![]() thẳng hàng.
thẳng hàng.
Bài tập
Bài 1: Cho ![]() ABC. Đường tròn nội tiếp
ABC. Đường tròn nội tiếp ![]() ABC tiếp xúc với AB, AC theo thứ tự tại M, N. Gọi E, F theo thứ tự là trung điểm của AC và BC. Tìm điểm P thuộc EF sao cho M, N, P thẳng hàng.
ABC tiếp xúc với AB, AC theo thứ tự tại M, N. Gọi E, F theo thứ tự là trung điểm của AC và BC. Tìm điểm P thuộc EF sao cho M, N, P thẳng hàng.
Bài 2: Cho ![]() ABC với O là tâm đường tròn ngoại tiếp tam giác đó. Các đường thẳng
ABC với O là tâm đường tròn ngoại tiếp tam giác đó. Các đường thẳng ![]() đôi một song song nhau lần lượt qua các điểm A, B, C và có giao điểm thứ hai với đường tròn (O) theo thứ tự là
đôi một song song nhau lần lượt qua các điểm A, B, C và có giao điểm thứ hai với đường tròn (O) theo thứ tự là ![]() . Chứng minh trực tâm của ba tam giác
. Chứng minh trực tâm của ba tam giác ![]() thẳng hàng.
thẳng hàng.
Bài 3: Cho hình bình hành ABCD. Gọi E là điểm đối xứng của D qua điểm A, F là điểm đối xứng của tâm O của hình bình hành qua điểm C và K là trung điểm của đoạn OB. Chứng minh ba điểm E, K, F thảng hàng và K là trung điểm của EF.
Bài 4: Cho tam giác ABC và M, N lần lượt là trung điểm AB, AC. Gọi P, Q là trung điểm MN và BC. CMR : A, P , Q thẳng hàng.
Hình học 10 - Tags: thẳng hàng, vecto