Bài tập chứng minh đẳng thức vectơ lớp 10 có lời giải
Chia sẻ phương pháp để làm các bài tập chứng minh đẳng thức vectơ trong chương trình lớp 10 qua lý thuyết và ví dụ có lời giải.
Ngoài việc nắm vững lý thuyết về các phép cộng, trừ, nhân vectơ với một số, tích vô hướng các em cần phải biết:
1) Lý thuyết vectơ áp dụng
+ Quy tắc 3 điểm: ![]() với mọi
với mọi ![]() .
.
+ Quy tắc hình bình hành: ![]() với
với ![]() là hình bình hành.
là hình bình hành.
+ Quy tắc trung điểm: ![]() với
với ![]() là trung điểm của
là trung điểm của ![]() .
.
+ Quy tắc trọng tâm: ![]() với
với ![]() là trong tâm tam giác
là trong tâm tam giác ![]() .
.
+ Các tính chất của các phép toán.
2) Phương pháp
+ Biến đổi vế này thành vế kia của đẳng thức (thông thường là xuất phát từ vế phức tạp biến đổi rút gọn để đưa về vế đơn giản hơn).
+ Biến đổi đẳng thức cần chứng minh về tương đương với một đẳng thức luôn đúng.
+ Xuất phát từ một đẳng thức luôn đúng để biến đổi về đẳng thức cần chứng minh.
– Chú ý: ![]() và
và ![]() có cùng trong tâm khi và chi
có cùng trong tâm khi và chi ![]()
Ví dụ 1: Cho 4 điểm ![]() . Chứng minh rằng:
. Chứng minh rằng:
a) ![]()
b) ![]()
Cách 1: Biến đổi vế trái (VT) ta có:
![]()
![]()
Nhận xét: Sử dụng cách giải này, ta cần chú ý khi biến đổi các số hạng của một vế cần quan tâm phân tích làm xuất hiện các số hạng có ở vế bên kia. Chẳng hạn số hạng ở vế trái là ![]() nhưng vế phải có chứa
nhưng vế phải có chứa ![]() nên ta viết
nên ta viết ![]()
Cách 2: Ta có:
![]()
Ta có (2) luôn đúng vậy (1) được chứng minh.
Cách 3: Ta có:
![]()
Suy ra ![]()
Do đó: ![]()
b) Ta có:
![]()
Tương tự ta cũng có các cách chứng minh khác cho câu b.
Ví dụ 2: Cho tam giác ![]() và
và ![]() là trong tâm tam giác
là trong tâm tam giác ![]() .
.
a) Chứng minh rằng: ![]()
b) Tìm tập hợp điểm ![]() sao cho
sao cho ![]()
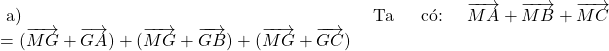
![]()
b) ![]()
![]() hay
hay ![]() do do
do do ![]()
Suy ra tập hợp ![]() thỏa mắn
thỏa mắn ![]() là
là ![]() .
.
3. Bài tập
Bài 1. Cho tứ diện ![]() . Gọi
. Gọi ![]() và
và ![]() lần lượt là trung điểm
lần lượt là trung điểm ![]() và
và ![]() Chứng minh:
Chứng minh:
a) ![]()
b) Điểm ![]() là trọng tâm của tứ diện
là trọng tâm của tứ diện ![]() khi và chỉ khi
khi và chỉ khi ![]()
Bài 2. Cho tứ diện ![]() với
với ![]() là trọng tâm.
là trọng tâm.
a) Chứng minh ![]()
b) Gọi ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Chứng minh:
. Chứng minh: ![]()
Bài 3. Cho hình hộp ![]() . Gọi
. Gọi ![]() ,
, ![]() ,
, ![]() lần lượt là điểm đối xứng của điểm
lần lượt là điểm đối xứng của điểm ![]() qua
qua ![]() ,
, ![]() ,
, ![]() . Chứng tỏ rằng
. Chứng tỏ rằng ![]() là trọng tâm của tứ diện
là trọng tâm của tứ diện ![]()
Bài 4. Cho hình hộp ![]() . Gọi
. Gọi ![]() lần lươt là điềm đối xứng của điểm
lần lươt là điềm đối xứng của điểm ![]() qua
qua ![]() Chứng tỏ rằng
Chứng tỏ rằng ![]() là trọng tâm của tứ diện
là trọng tâm của tứ diện ![]()
Bài 5. Cho hình chóp ![]() .
.
Chứng minh rằng nếu ![]() là hình bình hành thì
là hình bình hành thì ![]()
Gọi O là giao điểm của AC và BD . Chứng tỏ rằng ![]() là hình bình hành khi và chỉ khi
là hình bình hành khi và chỉ khi ![]()
