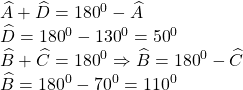Bài tập hình thang, hình thang vuông có lời giải

A. TÓM TẮT LÍ THUYẾT

1. Hình thang

Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

Hình thang   ABCD: AB // CD

Cạnh đáy:       AB, CD

Cạnh bên:       AD, BC

Đường cao:    AH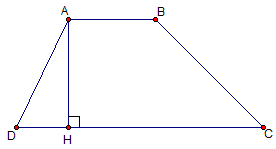

Bài tập hình thang, hình thang vuông có lời giải

Tính chất: trong một hình thang, góc kề một cạnh bên thì bù nhau.

Nhận xét:

+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau

2. Hình thang vuông

Định nghĩa: Hình thang vuông là hình thang có một cạnh bên vuông góc với hai đáy.

3. Dấu hiện nhận biết hình thang, hình thang vuông

+ Một tứ giác có hai cạnh song song là hình thang.

+ Hình thang có một góc vuông là hình thang vuông.

B. PHƯƠNG PHÁP GIẢI TOÁN

1. Dạng 1: Tính các góc của một hình thang

Bài 1: Cho hình thang ABCD có (AB//CD) có\displaystyle \widehat{A}-\widehat{D}={{20}^{0}}

và \displaystyle \widehat{B}=2\widehat{C} . Tính các góc của hình thang?

Hướng dẫn giải:

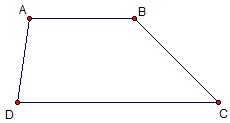Bài tập hình thang, hình thang vuông có lời giải-1ABCD là hình thang, AB//CD

+ \displaystyle \widehat{A}+\widehat{D}={{180}^{0}}(Hai góc kề cạnh bên bù nhau)
và \displaystyle \widehat{A}-\widehat{D}={{20}^{0}}

.  Suy ra: \displaystyle \widehat{A}={{100}^{0}} và \displaystyle \widehat{D}={{80}^{0}}

Mặt khác: \displaystyle \widehat{B}+\widehat{C}={{180}^{0}} (Hai góc kề cạnh bên bù nhau); \displaystyle \widehat{B}=2\widehat{C}

Suy ra: \displaystyle \widehat{C}={{60}^{0}} và \displaystyle \widehat{B}={{120}^{0}}.

Bài 2: Cho hình thang ABCD (AB//CD). Tính số đo các góc chưa biết.

Hướng dẫn giải:

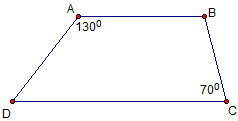Bài tập hình thang, hình thang vuông có lời giải-2ABCD hình thang, AB//CD

\displaystyle \begin{array}{l}\widehat{A}+\widehat{D}={{180}^{0}}-\widehat{A}\\\widehat{D}={{180}^{0}}-{{130}^{0}}={{50}^{0}}\\\widehat{B}+\widehat{C}={{180}^{0}}\Rightarrow \widehat{B}={{180}^{0}}-\widehat{C}\\\widehat{B}={{180}^{0}}-{{70}^{0}}={{110}^{0}}\end{array}

2. Dạng 2: Chứng minh một tứ giác là hình thang, hình thang vuông

Bài 3: Cho tứ giác ABCD, AB=BC và AC là tia phân giác của góc A. Chứng minh ABCD là hình thang.

Hướng dẫn giải:

Xét \displaystyle \Delta ABC:AB=BC (giả thuyết). Suy ra: \displaystyle \Delta ABC cân tại B

Từ đây suy ra: \displaystyle \widehat{{BAC}}=\widehat{{BCA}}

\displaystyle \widehat{{BAC}}=\widehat{{CAD}} (AD phân giác ).

Bài tập hình thang, hình thang vuông có lời giải-3Suy ra: \displaystyle \widehat{{BCA}}=\widehat{{CAD}}

Suy ra: \displaystyle BC//AD

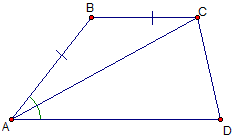Vậy tứ giác ABCD là hình thang.

Bài 4: Cho tam giác ABC vuông tại A, lấy điểm M thuộc cạnh BC sao cho \displaystyle AM=\frac{1}{2}BC, N là trung điểm cạnh AB. Chứng minh:

a. \displaystyle \Delta AMB cân

b. Tứ giác \displaystyle MNAC là hình thang vuông.

Hướng dẫn giải:

a. Chứng minh \displaystyle \Delta AMB cân:

Bài tập hình thang, hình thang vuông có lời giải-4Ta có  \displaystyle AM=\frac{1}{2}BC.    M thuộc cạnh BC.

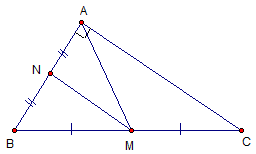Suy ra: M là trung điểm của cạnh BC.

\displaystyle \Rightarrow AM=MB=MC=\frac{{BC}}{2}

Suy ra:  \displaystyle \Delta AMB cân tại M

b. Chứng minh tứ giác \displaystyle MNAClà hình thang vuông:
Trong   \displaystyle \Delta AMB : AN = NB (giả thiết)

Suy ra:      \displaystyle MN\bot AB

\displaystyle AC\bot AB (\displaystyle \Delta ABC vuông tại A)

\displaystyle \Rightarrow MN//AC và \displaystyle \widehat{{CAN}}={{90}^{0}}

Suy ra: tứ giác \displaystyle MNAC là hình thang vuông.

Bài 5: Cho tứ giác ABCD và EFGH trên giấy kẻ ô vuông (hình vẽ). Quan sát rồi đoán nhận xem các tứ giác đó là hình gì, sau đó dùng thước và eke để kiểm tra lại dự đoán đó.

Bài tập hình thang, hình thang vuông có lời giải-5

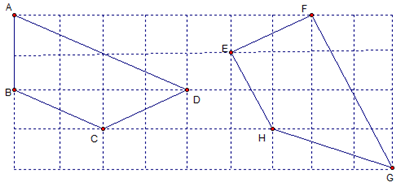
Hướng dẫn giải:

Tứ giác ABCD là hình thang ( vì BC // AD).

Tứ giác EFGH là hình thang vuông (\displaystyle \widehat{{H\text{EF}}}={{90}^{0}}và \displaystyle \widehat{{G\text{EF}}}={{90}^{0}}).

Bài 6:  Cho hình thang ABCD (AB // CD), các tia phân giác của góc A, góc D cắt nhau tại M thuộc cạnh BC. Cho biết AD = 7cm, chứng minh rằng một trong hai đáy của hình thang có độ dài nhỏ hơn 4cm.

Hướng dẫn giải:

* Tìm cách giải : Để chứng minh một cạnh đáy nào đó nhỏ hơn 4cm ta có thể xét tổng của hai cạnh đáy rồi chứng minh tổng này nhỏ hơn 8cm. Khi đó tồn tại một đáy có độ dài nhỏ hơn 4cm.

* Trình bày lời giải:

Gọi N là giao điểm của tia AM và tia DC.

Ta có AB // CD nên \displaystyle \widehat{{{{A}_{2}}}}=\widehat{N} (so le trong).

Mặt khác, \displaystyle \widehat{{{{A}_{1}}}}=\widehat{{{{A}_{2}}}} nên \displaystyle \widehat{{{{A}_{1}}}}=\widehat{N} Þ DDAN cân tại D .

Vì vậy: DA = DN.     (1)

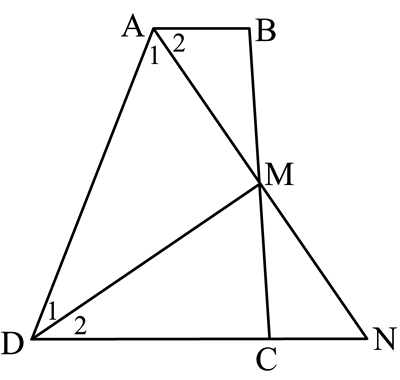Bài tập hình thang, hình thang vuông có lời giải-6Xét DDAN có \displaystyle \widehat{{{{D}_{1}}}}=\widehat{{{{D}_{2}}}}

Nên DM đồng thời là đường trung tuyến: MA = MN.

Nên: DABM = DNCM (g.c.g)

Do đó:  AB = CN.

Ta có :  DC + AB = DC + CN = DN = DA = 7cm. Vậy AB + CD < 8cm.

Vậy một trong hai đáy AB, CD phải có độ dài nhỏ hơn 4cm.

Bài 7: Dựng hình thang ABCD (AB // CD) biết: AB = 2cm, CD = 5cm, \displaystyle \widehat{C}={{40}^{o}};\displaystyle \widehat{D}={{70}^{o}}.

Hướng dẫn giải

a. Phân tích: Giả sử ta đã dựng được hình thang ABCD thoả mãn đề bài.

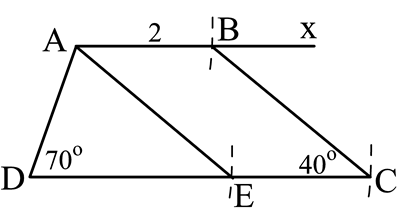Bài tập hình thang, hình thang vuông có lời giải-7Vẽ AE // BC (E ∈ CD).

Ta được: \displaystyle \widehat{{AED}}=\widehat{C}={{40}^{o}}, EC = AB = 2cm và DE = DC – EC = 5 – 2 = 3cm.

– DADE dựng được ngay (g.c.g).

– Điểm C thoả mãn hai điều kiện:
C nằm trên tia DE và C cách D là 5cm.

– Điểm B thoả mãn hai điều kiện: B nằm trên tia Ax // DE (hai tia Ax và DE cùng nằm trên một nửa mặt phẳng bờ AD) và B cách A là 2cm.

b. Cách dựng:
– Dựng ΔADE sao cho DE = 3cm; \displaystyle \widehat{D}={{70}^{o}};\displaystyle \widehat{E}={{40}^{o}}.

– Dựng tia Ax // DE (hai tia Ax và DE cùng nằm trên một nửa mặt phẳng bờ AD).

– Trên tia Ax đặt AB = 2cm.

– Trên tia DE đặt DC = 5cm.

– Nối BC ta được hình thang ABCD phải dựng.

c. Chứng minh:
Theo cách dựng tứ giác ABCD có AB // CD nên nó là hình thang.

Xét hình thang ABCE có CE = 5 – 3 = 2(cm);

AB = 2cm nên AB = CE do đó AE // BC \displaystyle \Rightarrow \widehat{{BCD}}=\widehat{{AED}}={{40}^{o}}.

Như vậy hình thang ABCD có AB = 2cm; CD = 5cm; \displaystyle \widehat{D}={{70}^{o}} và \displaystyle \widehat{C}={{40}^{o}}.

d. Biện luận: Bài toán có một nghiệm hình.

Bài 8: Dựng tam giác ABC, biết \displaystyle \widehat{A}={{70}^{o}}, BC = 5cm và AC – AB = 2cm.

Hướng dẫn giải

a) Phân tích: Giả sử ta đã dựng được tam giác ABC thoả mãn đề bài.
Trên tia AC ta lấy điểm D sao cho AD = AB.

Khi đó DC = AC – AD = AC – AB = 2cm.

ΔABD cân, \displaystyle \widehat{A}={{70}^{o}}\displaystyle \Rightarrow \widehat{{ADB}}={{55}^{o}}\displaystyle \Rightarrow \widehat{{BDC}}={{125}^{o}}.

– ΔDBC xác định được (CD = 2cm; \displaystyle \widehat{D}={{125}^{o}}; CB = 5cm).

– Điểm A thoả mãn hai điều kiện:

A nằm trên tia CD và A nằm trên đường trung trực của BD.

b) Cách dựng

– Dựng ΔDBC sao cho \displaystyle \widehat{D}={{125}^{o}}; DC = 2cm và CB = 5cm.

– Dựng đường trung trực của BD cắt tia CD tại A.

– Nối AB ta được DABC phải dựng.

c) Chứng minh

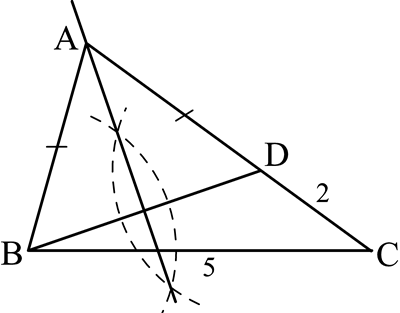Bài tập hình thang, hình thang vuông có lời giải-8Ta có: ΔABC thoả mãn đề bài vì theo cách dựng, điểm A nằm trên đường trung trực của BD nên AD = AB.

Do đó AC – AB = AC – AD = DC = 2cm;
BC = 5cm và \displaystyle \widehat{{ADB}}={{180}^{o}}-{{125}^{o}}={{55}^{o}}

\displaystyle \Rightarrow \widehat{{BAC}}={{180}^{o}}-{{2.55}^{o}}={{70}^{o}}.

d) Biện luận : Bài toán có một nghiệm hình.

Nhận xét: Đề bài có cho đoạn thẳng 2cm nhưng trên hình vẽ chưa có đoạn thẳng nào như vậy. Ta đã làm xuất hiện đoạn thẳng DC = 2cm bằng cách trên AC ta đặt AD = AB. Khi đó DC chính là hiệu AC – AB.

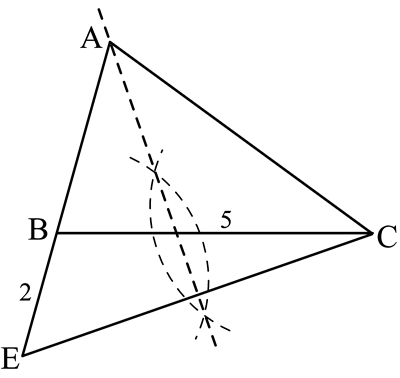Bài tập hình thang, hình thang vuông có lời giải-9Cũng có thể làm xuất hiện đoạn thẳng 2cm bằng cách trên tia AB ta đặt AE = AC

Khi đó BE = AE – AB = AC – AB = 2cm.

DAEC cân, có \displaystyle \widehat{A}={{70}^{o}}

\displaystyle \Rightarrow \widehat{E}=\left( {{{{180}}^{o}}-{{{70}}^{o}}} \right):2={{55}^{o}}.

DBEC xác định được.

Khi đó điểm A thoả mãn hai điều kiện:

A nằm trên tia EB và A nằm trên đường trung trực của EC.

C. Bài tập tự giải

Bài tập 1: Cho hình thang ABCD (AB//CD), AB<CD, AD=BC=AB, \displaystyle \widehat{{BDC}}={{30}^{0}}. Tính các góc của hình thang.

Bài tập 2: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ \displaystyle HD\bot AC,HE\bot AB. Gọi M, N lần lượt là trung điểm của các đoạn thẳng HB, HC. Chứng minh tứ giác DEMN là hình thang vuông.

Bài tập 3: Cho hình thang ABCD  \displaystyle \left( {AB//CD} \right). Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy CD. Chứng minh AD+BC=DC.

Bài tập 4: Cho hình thang ABCD vuông tại A và D. Cho biết AD = 20, AC = 52 và  BC = 29. Tính độ dài AB.

Bài tập 5: Cho tứ giác ABCD. Các tia phân giác của góc A, góc D cắt nhau tại M. Các tia phân giác của B, góc C cắt nhau tại N. Cho biết \displaystyle \widehat{{AMD}}={{90}^{o}}, chứng minh rằng:

a) Tứ giác ABCD là hình thang;

b) NB ⊥ NC

Bài tập 6: Cho hình thang ABCD vuông tại A và D. Gọi M là trung điểm của AD.  Cho biết MB ⊥ MC.    a. Chứng minh rằng BC = AB + CD;

b. Vẽ MH ⊥ BC. Chứng minh rằng tứ giác MBHD là hình thang.
Bài tập 7: Chứng minh rằng trong một hình thang vuông, hiệu các bình phương của hai đường chéo bằng hiệu các bình phương của hai đáy.

Hình học 8 - Tags: , ,