Bài tập nhân hai lũy thừa cùng cơ số
Lý thuyết:
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của một số a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
![]() = a.a…a (n ≠ 0)
= a.a…a (n ≠ 0)
a gọi là cơ số, n gọi là số mũ. Quy ước ![]() .
.
![]() còn được gọi là bình phương của a.
còn được gọi là bình phương của a.
![]() còn được gọi là lập phương của a.
còn được gọi là lập phương của a.
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Cách nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: ![]() .
.
Cách nhận biết số chính phương
Một số là bình phương của một số tự nhiên được gọi là số chính phương.
Ví dụ:
9 là số chính phương vì 9 = ![]() .
.
16 là số chính phương vì ![]() .
.
Các dạng toán
Dạng 1. Viết gọn một tích bằng cách dùng lũy thừa
Phương pháp giải
Áp dụng công thức:

Ví dụ 1. (Bài 56 trang 27 SGK)
Viết gọn các tích sau bằng cách dùng lũy thừa :
a) 5.5.5 5.5.5 ; b) 6.6.6.3.2 ;
c) 2 2.2.3.3 ; d) 100.10.10.10.
Giải
a) 5.5.5.5.5.5 = 56
b) 6.6.3.2 = 6.6.6.6 = 64 ;
c) 2.2.3.3 = 23.32 ;
d) 100.10.10.10 = 10.10.10.10.10 = 105 .
Ví dụ 2. (Bài 57 trang 28 SGK)
Tính giá trị các lũy thừa sau :
a) 23, 24,25,26,27,28,29,210 ;
b) 32, 33,34,35 ;
c) 42,43,44;
d) 52,53,54;
e) 62, 63,64.
Giải
a) 23 = 2.2.2 = 8 ; 24 = 23.2 = 8.2 = 16.
Làm tương tự như trên ta được :
25 = 32 , 26 = 64 , 27 = 128 , 28 = 256, 29 = 512 , 210 = 1024.
b) 32 = 9, 33 = 27 , 34 = 81, 35 = 243 .
c) 42 = 16, 43 = 64, 44 = 256 .
d) 52 = 25, 53 = 125, 54 = 625.
e) 62 = 36, 63 = 216, 64 = 1296.
Ví dụ 3. (Bài 58a và 59a trang 28 SGK)
58a) Lập bảng bình phương của các số tự nhiên từ 0 đến 20.
59a) Lập bảng lập phương của các số tự nhiên từ 0 đến 10.
Giải
58a) Lập bảng bình phương của các số tự nhiên từ 0 đến 20.
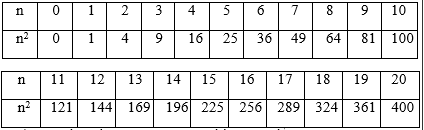
59a) Lập bảng lập phương của các số tự nhiên từ 0 đến 10.

Ví dụ 4. Nhà văn Anh sếch-xpia (1564-1616) đã viết a2 cuốn sách, trong đó a là số tự
nhiên lớn nhất có hai chữ số.
Tính số sách sếch-xpia đã viết.
Giải
Số tự nhiên lớn nhất có hai chữ số là 99 nên a = 99. Do đó a2 = 992 = 9801.
Số sách sếch-xpia đã viết là 9801 cuốn.
Ví dụ 5. (Bài 62a trang 28 SGK)
Tính 102 ; 103 ; 104 ; 105 ; 106.
Đáp số
102 = 100 ; 103 = 1000 ; 104 = 10000 ; 105 = 100000 ; 106 = 1000 000.
Ví dụ 6. (Bài 65 trang 29 SGK)
Bằng cách tính, em hãy cho biết số nào lớn hơn trong hai số sau ?
a) 23 và 32 ; b) 24 và 42 ;
c)25 và 52; d) 210 và 100.
Giải
a) 23 = 8, 32 = 9 . Vì 8 < 9 nên 23 < 32 .
b) 24 =16 , 42=16 nên 24 = 42.
c) 25 = 32 , 52 = 25 nên 25 > 52.
d) 210 = 1024 nên 210 >100.
Ví dụ 7. (Bài 66 trang 29 SGK)
Đố : Ta biết 112 =121 ; 1112 =12321. Hãy dự đoán : 1111a bằng bao nhiêu ? Kiểm tra lại dự
đoán đó.
Đáp số
11112 = 1234321.
Dạng 2. Viết một số dưới dạng một lũy thừa với số mũ lớn hơn 1
Ví dụ 8. (Bài 58 b; 59b trang 28 SGK)
58b) Viết mỗi số sau thành bình phương của một số tự nhiên : 64 ; 169 ; 196.
59b) Viết mỗi số sau thành lập phương của một số tự nhiên : 27 ; 125 ; 216.
Giải
58b) 64 = 8.8 = 82; 169 = 13.13 = 132 ; 196 = 14.14 = 142.
59b) 27 = 3.3,3 = 33 ; 125 = 5.5.5 = 53 ; 216 = 6.6.6 = 63.
Ví dụ 9. (Bài 61 trang 28 SGK)
Trong các số sau, số nào là lũy thừa của một số tự nhiên với số mũ lớn hơn 1 (chú ý rằng
có những số có nhiều cách viết dưới dạng lũy thừa) : 8, 16, 20, 27, 60, 64, 81, 90, 100.
Đáp số
8 = 23; 16 = 42 = 24 ;
27 = 33 ; 64 = 82 – 26 = 43;
81 = 92 = 34; 100 = 102.
Ví dụ 10. (Bài 62b trang 28 SGK)
Viết mỗi số sau dưới dạng lũy thừa của 10 : 1000 ; 1 000 000;
![]()
Đáp số
1000 = 103;
1 000 000 = 106;
1 tỉ = 109;
![]()
Dạng 3. Nhân hai lũy thừa cùng cơ số
Phương pháp giải
Áp dụng công thức : am.an = am+n (a,m,n ∈ N).
Ví dụ 11. (Bài 60 trang 28 SGK)
Viết kết quả phép tính sau dưới dạng một lũy thừa :
a) 33.34 ; b) 52.57; c) 75.7.
Giải
a) 33.34 = 33+4 = 37 ;
b) 52.57 = 52+7 = 59 ;
c) 75.7 = 75+1 – 76
Ví dụ 12. (Bài 63 trang 28 SGK)
Điền dấu “ x ” vào ô thích hợp :

Giải

Ví dụ 13. (Bài 64 trang 29 SGK)
Viết kết quả phép tính dưới dạng một lũy thừa :
a) 23.22.24;
b) 102.103.105 ;
c) x . x5 ;
d) a3.a2.a5 ;
Giải
a) 23.22.24 = 23+2+4 = 29 ;
b) 102.103.105 = 102+3+5 = 1010;
c) x = x5 = x1+5 – x6;
d) a3.a2.a5 = a3+2+5 = 210 ;
Bài tập:
Bài 1. Viết dưới dạng lũy thừa :
a) 3.3.3.3.3 ; b) y.y.y.y ;
c) 2.x.2.x.2.x.x ; d) a.a b.b c.c.c.c
Bài 2. Tìm giá trị của các lũy thừa sau :
a) 27; b) 3 ; c) 44; d)55.
Bài 3. Số nào lớn hơn trong hai số sau :
a) 26 và 62 ; b) 34 và 43 ; c) 54 và 45.
Bài 4. Hãy dự đoán 111112 và 1111112 bằng bao nhiêu ?
Bài 5. Viết mỗi sô sau thành một bình phương : 81 , 121 , 225 , 10 000.
Bài 6. Viết mỗi số sau thầnh một lập phương : 0 , 64 , 343 , 1 000 000.
Bài 7. Trong các số sau, số nào là lũy thừa của một số tự nhiên với số mũ lớn hơn 1 : 9 , 15 , 16 , 256 , 300 ?
Bài 8. Viết mỗi số sau dưới dạng lũy thừa của 10 :1000 ;
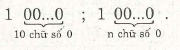
Bài 9. Viết các tích các lũy thừa sau đây dưới dạng một lũy thừa :
a) 23.24.2 ; b) 52.57.53 ; c) 30.35.37.
Bài 10. So sánh các lũy thừa sau đây :
a) 1112 và 1113 ; b) 74 và 84 ; c) (6 – 5)432 và (7-6)543.
Bài 11.
Dùng lũy thừa để viết gọn kết quả của phép nhân :
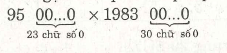
Bài 12.
Tính giá trị của các biểu thức : A = 32.33 23.22 ; B = 3.42 – 22.3
Bài 13.
Tính giá trị các biểu thức : C = 210-2 ; D = (8.9)2 ; E = 28-1. Nhận xét về các chữ số ở kết quả và các chữ số ở biểu thức đã cho.
Bài 14. So sánh :
a) (3 + 7) và 33 + 73; b) 48.(4 + 8) và 43 + 83;
c) (14 + 7) và 143 + 73 ; d) 111.(11 + 1) và 113 +13.
Bài 15. Dùng máy tính bỏ túi kiểm tra các đẳng thức sau
a) 122 +322 +432 +562 +672 +872 = 782 + 762 +652 + 342 + 232 + 212.
b) 123 + 323 + 433 + 563 + 673 + 873 = 783 + 763 + 653 + 343 + 233 + 213.
Bài 16. Dùng máy tính bỏ túi kiểm tra các đẳng thức sau :
a) 9801 = (98 + 01)2 ; b) 3025 = (30 + 25)2.
Bài 17. Viết các tổng sau thành một bình phương :
13 + 23 – 3 + 43 + 53; b) 13 + 23 + 33 + 43 + 53 + 63 .
Số học 6 - Tags: cơ số, lũy thừa, toán 6Các dạng toán về Tập hợp – Số học 6
Bài tập chia hai lũy thừa cùng cơ số
Phương pháp giải các dạng toán phân số lớp 6
32 bài tập cơ bản và nâng cao Số học 6 có đáp án
Lũy thừa và số mũ tự nhiên. Nhân hai lũy thừa cùng cơ số
Khái niệm, tính chất cơ bản, rút gọn phân số
Quy tắc cộng, trừ, nhân, chia số nguyên
