Bảng công thức tính nguyên hàm
Bảng tóm tắt công thức tính nguyên hàm cơ bản, mở rộng và nâng cao đầy đủ nhất. Giúp học sinh 12 ghi nhớ các nguyên hàm dễ dàng.
Định nghĩa nguyên hàm:
Cho hàm số f xác định trên K. Hàm số F được gọi là nguyên hàm của hàm số f trên K nếu F(x) khả vi trên K và F'(x) = f(x) với mọi x ∈ K.
Ví dụ: Hàm số f(x) = cos X có nguyên hàm là F (X) = sin X vi (sin X)’ = cos X (tức F ‘(X) = f (X)).
Các công thức nguyên hàm có trong bảng dưới đây:
– Nguyên hàm vô tỷ
– Nguyên hàm hữu tỉ
– Nguyên hàm mũ e
– Nguyên hàm logarit
– Nguyên hàm lượng giác
Công thức nguyên hàm cơ bản thường gặp
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
Công thức nguyên hàm mở rộng (a ≠ 0)
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21.
![]()
![]()
![]()
![]()
![]()
Bảng các nguyên hàm nâng cao (a ≠ 0)
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. ![]()
27. 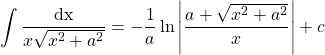
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
