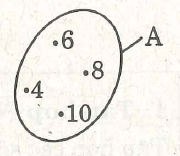Các dạng toán về Tập hợp – Số học 6
A. Lý thuyết
1. Mỗi đối tượng trong một tập hợp là một phần tử của tập hợp đó. Kí hiệu :
a ∈ A (a thuộc A hoặc a là phần tử của tập hợp A)
b ∈ A (b không thuộc A hoặc b không phải là phần tử của tập hợp A).
2. Để biểu diễn một tập hợp, ta có thể :
Liệt kê các phần tử của tập hợp ;
Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
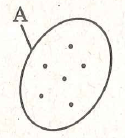
3. Tập hợp được minh họa bởi một vòng tròn, trong đó mỗi phần tử của tập hợp được biểu diễn bởi
một dấu chấm bên trong. Hình minh họa tập hợp như vậy gọi là biểu đồ Ven.
B. Các dạng toán
Dạng 1. Viết một tập hợp cho trước
Phương pháp giải:
Dùng một chữ cái in hoa và dấu ngoặc nhọn, ta có thể viết một tập hợp theo hai cách :
- Liệt kê các phần tử của nó.
- Chỉ ra tính chất đặc trưng cho các phần tử của nó.
Ví dụ 1. (Bài 2 trang 6 SGK)
Viết tập hợp các chữ cái trong từ “TOÁN HỌC”.
Giải
{ T, O, A, N, H, C}
Chú ý : Mỗi phần tử của tập hợp chỉ liệt kê một lần.
Ví dụ 2. (Bài 4 trang 6 SGK)
Nhìn các hình 3, 4 và 5, viết các tập hợp A, B, M, H.
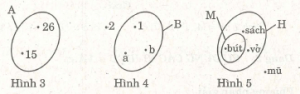
A = {15; 26}; B = {1; a ; b}; M = {bút}; H = {bút, sách, vở}.
Chú ý:
– Trong các hình vẽ minh họa tập hợp, mỗi phần tử của tập hợp được biểu diễn bởi một dấu chấm
bên trong vòng tròn.
– Các phần tử của một tập hợp được viết cách nhau bởi dấu hoặc dấu “;” hoặc dấu “,”. Trong
trường hợp các phần tử của tập hợp không phải là số , ta thường dùng dấu phẩy. Trong trường
hợp có một phần tử của tập hợp là số, ta thường dùng dấu chấm phẩy nhằm tránh nhầm lẫn
giữa số tự nhiên và sốthập phân.
Ví dụ 3. (Bài 5 trang 6 SGK)
a) Một năm gồm bốn quý. Viết tập hợp A các tháng của quý hai trong năm.
b) Viết tập hợp B các tháng (dương lịch) có 30 ngày.
Giải
a) A = {tháng tư, tháng năm, tháng sáu}.
b) B = {tháng tư, tháng sáu, tháng chín, tháng mười một}.
Ví dụ 4. Viết tập hợp M các số tự nhiên có một chữ số.
Giải
Ta có thể viết tập hợp M theo hai cách :
Cách 1 : M = {0 ; 1; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9} .
Cách 2 : M = {x ∈ N / x < 10} (N là kí hiệu tập hợp các số tự nhiên).
Ví dụ 5. Cho p là tập hợp các số tự nhiên lớn hơn 3 và nhỏ hơn 8. Hãy viết tập hợp p theo hai
cách.
Giải
Cách 1 : p = {4 ; 5 ; 6 ; 7}.
Cách 2 : p = {x ∈ N / 3 < x < 8}.
Dạng 2. Sử dụng các kí hiệu ∈ và ∉
Phương pháp giải
Nắm vững ý nghĩa các kí hiệu ∈ và ∉.
Kí hiệu ∈ đọc là “là phần tử của” hoặc “thuộc”.
Kí hiệu ∉ đọc là “không phải là phần tử của” hoặc “không thuộc”.
Ví dụ 6. (Bài 1 trang 6 SGK)
Viết tập hợp A các số tự nhiên lớn hơn 8 và nhỏ hơn 14 bằng hai cách, sau đó điền kí hiệu thích
hợp vào chỗ chấm : 12 … A ; 16 … A.
Giải
A = {9 ; 10 ; 11 ; 12 ; 13} hoặc A = {x 6∈ N/ 8 < x < 14} ;
12 ∈ A ;
16 ∉ A.
Ví dụ 7. (Bài 3 trang 6 SGK)
Cho hai tập hợp : A = {a, b} ; B = {b, x, y}. Điền kí hiệu thích hợp vào chỗ chấm :
x … A ; y … B ; b … A ; b … B.
Giải
x ∈ A ; y ∈ B ; b ∈ A ; b ∈ B.
Ví dụ 8. Cho ba tập hợp :
A = {gà, vịt, ngan, ngỗng} ;
B = {chó, mèo, chim) ;
C = {ngan, gà, vịt}.
Trong các cách viết sau, cách nào đúng, cách nào sai:
a) gà ∈ A ; b) vịt ∈ B ; c) ngỗng ∈ C ;
d) chó ∉ A; e) mèo ∈ B ; f) gà ∉ C ;
g) ngan ∈ A ; h) chim ∈ B ; i) vịt ∉ C .
Giải.
Các cách viết trong các câu sau đây là đúng : a), d), e), g), h). Các câu hỏi còn lại viết sai.
Dạng 3. Minh họa một tập hợp cho trước bằng hình vẽ
Phương pháp giải
Sử dụng biểu đồ Ven. Đó là một đường cong khép kín, không tự cắt, mỗi phần tử của tập hợp
được biểu diễn bởi một điểm ở bên trong đường cong đó.
Ví dụ 9. Gọi A là tập hợp các số tự nhiên chẵn m sao cho 4 < m < 11 Hãy minh họa tập hợp A bằng
hình vẽ.
Giải
Xem hình bên.