Cách chứng minh 2 đường thẳng vuông góc bằng vectơ
Để chứng minh cho hai đường thẳng vuông góc bằng vectơ, chúng ta chứng minh tích vô hướng của chúng bằng 0.
Tức là: ![]()
Xét ví dụ có lời giải dưới đây.
Ứng dụng vectơ chứng minh vuông góc
Bài toán: Trong đường tròn C(O; R) cho hai dây cung AA’, BB’ vuông góc với nhau ở điểm S và gọi M là trung điểm của AB. CMR: SM vuông góc A’B’.
Giải
Xét tích vô hướng
![]()
![]()
Ta có:
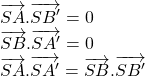
Từ đó suy ra ![]() nên SM vuông góc với A’B.
nên SM vuông góc với A’B.
Bài tập
Bài 1: Gọi ![]() là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp ![]() ,
, ![]() là trung điểm cạnh
là trung điểm cạnh ![]() ,
, ![]() là trọng tâm của
là trọng tâm của ![]() . Chứng minh rằng nếu
. Chứng minh rằng nếu ![]() thì
thì ![]() .
.
Bài 2: Cho ![]() cân tại
cân tại ![]() Gọi
Gọi ![]() là trung điểm cạnh
là trung điểm cạnh ![]() ,
, ![]() là trọng tâm
là trọng tâm ![]() . Chứng minh
. Chứng minh ![]() . (
. (![]() là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp ![]() ).
).
Bài 3: Cho tam giác ABC có hai trung tuyến BM và CN. Chứng minh rằng: ![]()
Bài 4: Cho hình chữ nhật ![]() , kẻ
, kẻ ![]() . Gọi M,N lần lượt là trung điểm của AH và DC. Chứng minh rằng:
. Gọi M,N lần lượt là trung điểm của AH và DC. Chứng minh rằng: ![]() .
.
