Cách chứng minh đường trung tuyến trong tam giác

Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.

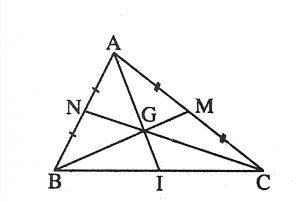
Tam giác ABC có các đường trung tuyến AI, BM, CN

Định lý 1: Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

Định lý 2: Khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó.

Định lý 3: Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.

Ví dụ: Tam giác ABC có G là trọng tâm

AG = 2/3 AI; BG = 2/3 BM; CG = 2/3 CN

GI = 1/3 AI; GM = 1/3 BM; GN = 1/3 CN

Tính chất 1: Trong tam giác cân (hoặc tam giác đều) đường trung tuyến ứng với cạnh đáy chia tam giác thành hai tam giác bằng nhau.

Ví dụ: Tam giác ABC cân có AD là đường trung tuyến

=> Diện tích ABD = ACD

Tính chất 2: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng ½ cạnh huyền.

Ví dụ: Tam giác ABC vuông tại A có AM là đường trung tuyến

=> AM = MB = MC = 1/2 BC

– Cách 1: Chứng minh đường đó nối một đỉnh của tam giác với trung điểm cạnh đối diện.

Ví dụ: Tam giác ABC có D là trung điểm BC

=> AD là đường trung tuyến của tam giác ABC

– Cách 2: Chứng minh khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó.

Ví dụ: Tam giác ABC có điểm G thỏa mãn AG = 2/3 AD (D ∈ BC)

=> AD là đường trung tuyến của tam giác ABC

– Cách 3: Chứng minh khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.

Ví dụ: Tam giác ABC có điểm G thỏa mãn GD = 1/3 AD (D ∈ BC)

=> AD là đường trung tuyến của tam giác ABC