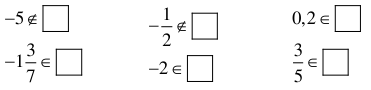Dạng bài tập: Nhận biết số hữu tỉ – Đại số 7

Muốn xác định xem một số có phải số hữu tỉ không, ta hãy biến đổi xem số đó có dạng a/b với a, b ∈ Z; b ≠ 0 hay không.

Từ đó suy ra phương pháp chứng minh một số là số hữu tỉ: Để nhận biết một số là số hữu tỉ ta biến đổi xem số đó có dạng a/b với a, b ∈ Z; b ≠ 0  hay không. Nếu có thì kết luận là số hữu tỉ, nếu không thì kết luận là số vô tỉ.

Ví dụ:

Các số 0,7; \displaystyle -1,2;

\displaystyle 1\frac{3}{4}; \displaystyle 2\frac{7}{8} là số hữu tỉ vì chúng biểu diễn được dưới dạng phân số a/b với a, b ∈ Z; b ≠ 0:

\displaystyle \displaystyle 0,7=\frac{7}{{10}}

Tương tự \displaystyle \displaystyle -1,2=\frac{{-12}}{{10}}

….

Bài tập:

Bài 1: Các số \displaystyle -2,4;\displaystyle -1\frac{3}{4};\displaystyle -5 có phải là các số hữu tỉ không? Vì sao?

Bài 2: Các số thập phân vô hạn tuần hoàn \displaystyle 0,\left( 3 \right);\displaystyle -1,2\left( {34} \right);\displaystyle -0,\left( 4 \right) có là các số hữu tỉ không? Vì sao?

Hướng dẫn:

Nhận xét: \displaystyle 0,\left( 1 \right)=\frac{1}{9};\displaystyle 0,\left( {01} \right)=\frac{1}{{99}} nên \displaystyle 0,\left( 3 \right)=3.0,\left( 1 \right)=3.\frac{1}{9}=\frac{3}{9}

\displaystyle -1,2\left( {34} \right)=-\left( {1,2+0,0\left( {34} \right)} \right)

\displaystyle {=-\left( {\frac{{12}}{{10}}+\frac{{34}}{{10}}.0,\left( {01} \right)} \right)}

\displaystyle {=-\left( {\frac{{12}}{{10}}+\frac{{34}}{{10}}.\frac{1}{{99}}} \right)}

\displaystyle {=-\frac{{1222}}{{990}}=-\frac{{611}}{{495}}}

Vậy \displaystyle 0,\left( 3 \right);\displaystyle -1,2\left( {34} \right);\displaystyle -0,\left( 4 \right) đều là số hữu tỉ.

Bài 3: Điền kí hiệu \displaystyle \left( {\in ,\,\,\notin ,\,\,\subset } \right) thích hợp vào ô vuông

Dạng bài tập: Nhận biết số hữu tỉ - Đại số 7

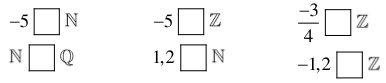
Bài 4: Điền tên các tập hợp \displaystyle \left( {\mathbb{N},\,\,\mathbb{Z},\,\,\mathbb{Q}} \right) vào ô vuông

Dạng bài tập: Nhận biết số hữu tỉ - Đại số 7-1

Đại số 7 - Tags: