Định nghĩa, tính chất, cách chứng minh tam giác cân

Định nghĩa tam giác cân

Tam giác cân là tam giác có 2 cạnh bên bằng nhau.

Định nghĩa, tính chất, cách chứng minh tam giác cân

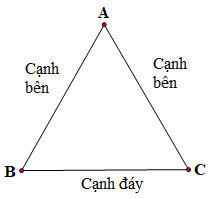
Tam giác cân ABC cân tại A

Từ hình vẽ, ta xác định được:

– Đỉnh A của tam giác cân ABC là giao điểm của hai cạnh bên AB và AC.

– Góc A được gọi là góc ở đỉnh, hai góc còn lại B và C là góc đáy.

Cách dựng tam giác ABC cân tại A

– Vẽ cạnh BC

– Vẽ cung tròn tâm B, bán kính r

– Vẽ cung tròn tâm C, bán kính r

Hai cung tròn cắt nhau tại A.

Tam giác ABC là tam giác cần vẽ.

Tính chất của tam giác cân

– Tính chất 1: Trong tam giác cân, hai góc đáy bằng nhau.

Ví dụ: Tam giác ABC cân tại A ⇒ Góc B = C

– Tính chất 2: Tam giác có hai góc bằng nhau là tam giác cân.

Ví dụ: Tam giác ABC có góc B = C ⇒ Tam giác ABC cân tại A

– Tính chất 3: Trường hợp đặc biệt của tam giác cân:

Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Ví dụ: Tam giác MNP vuông tại M có góc N = P ⇒ Tam giác MNP vuông cân tại M

Tính số đo mỗi góc nhọn của tam giác vuông cân.

Ta có: Δ ABC có Góc A = 90°, Góc B = C

⇒ Góc B + C = 90° (định lí tổng ba góc của một tam giác)

⇒ 2.Ĉ = 90°

⇒ Góc B = C = 45°

Kết luận: Tam giác vuông cân thì hai góc nhọn bằng 45°.

Cách chứng minh tam giác cân

Để chứng minh một tam giác là tam giác cân ta sử dụng một trong hai cách sau:

– Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau.

– Cách 2: Chứng minh tam giác đó có hai góc bằng nhau.

Xem ví dụ dưới đây để nắm được cách chứng minh tam giác cân.

Ví dụ: Trong tam giác ABC có ΔABM = ΔACM . Chứng minh tam giác ABC cân.

Định nghĩa, tính chất, cách chứng minh tam giác cân

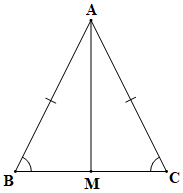
Chứng minh tam giác ABC cân

+ Chứng minh theo cách 1:

Theo bài ra, ta có:

ΔABM = ΔACM

⇒ AB = AC

⇒ Tam giác ABC cân tại A

+ Chứng minh theo cách 2:

Theo bài ra, ta có:

∆ABM = ∆ACM

⇒ Góc B = C

⇒ Tam giác ABC cân tại A

Hình học 7 - Tags: ,