Nguyên hàm đa thức tính như nào?
Cách tính nguyên hàm của đa thức như thế nào? Cần phải áp dụng các công thức gì để tính nguyên hàm đa thức?
Tính nguyên hàm của hàm số là đa thức là dạng cơ bản nhất trong chương nguyên hàm – Toán 12.
Công thức tính nguyên hàm đa thức thường dùng
![]()
![]()
![]()
Trong đó, k là hằng số.
![]()
Cách tính nguyên hàm của đa thức
Xem chi tiết các bài tập nguyên hàm có lời giải dưới đây.
Bài tập 1. Họ nguyên hàm của hàm số ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải:
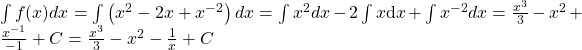
⇒ Chọn đáp án C.
Bài tập 2. Trong các hàm số sau đây, hàm số nào là một nguyên hàm của hàm số: ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải:
Ta có:
![]()
![]()
![]()
![]()
⇒ Chọn đáp án D.
Bài tập 3. Nguyên hàm F(x) của hàm số ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải:
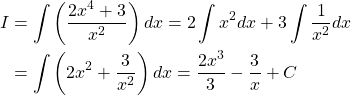
⇒ Chọn đáp án A.
Bài tập 4. Nguyên hàm F(x) của hàm số ![]() là
là
A. ![]()
B. ![]()
C. 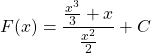
D. 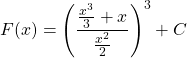
Giải:
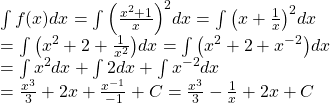
⇒ Chọn đáp án A.
Bài tập 5. Tìm hàm số ![]() biết rằng
biết rằng ![]() và
và ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Theo giả thiết ta có:
![]()
Vậy hàm số cần tìm là ![]()
