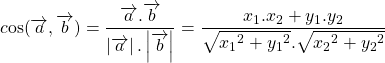Tích vô hướng của hai vectơ

Contents

Định nghĩa

Tích vô hướng của hai vectơ \overrightarrow{a}, \overrightarrow{b} là một số, kí hiệu là \overrightarrow{a}.\overrightarrow{b} được xác định bởi:

\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|.c\text{os}\left( \overrightarrow{a},\overrightarrow{b} \right)

Hệ quả

– Bình phương vô hướng của vectơ \overrightarrow{a}: \overrightarrow{{{a}^{2}}}={{\left| \overrightarrow{a} \right|}^{2}}

– Điều kiện vuông góc của hai vectơ: \overrightarrow{a}\bot \overrightarrow{b}\Leftrightarrow \overrightarrow{a}.\overrightarrow{b}=0

Tính chất

Với mọi \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c} và số thực k:

–  \overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a};

– (m.\overrightarrow{a}).\overrightarrow{b}=m(\overrightarrow{a}.\overrightarrow{b});

– \overrightarrow{a}.(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c};

Biểu thức tọa độ tích vô hướng của hai vectơ

Trong mặt phẳng tọa độ Oxy, cho hai vectơ \overrightarrow{a}({{x}_{1}};{{y}_{1}}), \overrightarrow{b}({{x}_{2}};{{y}_{2}}).

Khi đó \overrightarrow{a}.\overrightarrow{b}={{x}_{1}}.{{x}_{2}}+{{y}_{1}}.{{y}_{2}}

Hệ quả:

– \displaystyle \left| \overrightarrow{a} \right|=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}

– \displaystyle c\text{os}(\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}=\frac{{{x}_{1}}.{{x}_{2}}+{{y}_{1}}.{{y}_{2}}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}.\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}

Hình học 10 - Tags: ,