Bài tập: Đường tròn, Tam giác – Hình học 6
Khái niệm đường tròn là gì? Hình tròn là gì? Điểm nằm trong, nằm ngoài đường tròn, dây cung của đường tròn. Định nghĩa tam giác ABC.
Dưới đây là lý thuyết và bài tập về chuyên đề: Đường tròn và Tam giác trong chương trình Hình học 6.
Đường tròn
Khái niệm đường tròn
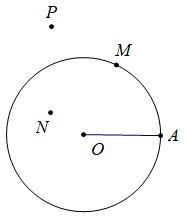
Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu (O; R).
![]()
– N nằm bên trong ![]()
– P nằm bên ngoài ![]()
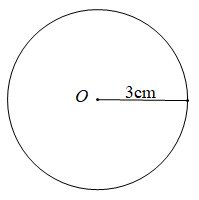
Ví dụ: Đường tròn tâm O bán kính 3cm kí hiệu là (O; 3cm)
Khái niệm hình tròn
Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm trong đường tròn đó.
Ví dụ: Cái đĩa, đồng hồ, …
Dây cung
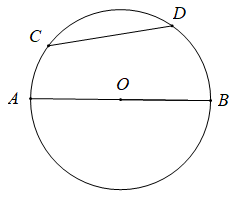
Hai điểm C, D của một đường tròn chia đường tròn thành hai cung. Đoạn thẳng nối hai mút của một cung là dây cung. Dây cung đi qua tâm là đường kính.
Ví dụ: Đoạn thẳng CD là dây cung, đoạn thẳng AB là đường kính.
Tam giác
Định nghĩa tam giác
Tam giác ABC là hình gồm ba đoạn thẳng AB, BC, CA khi A, B, C không thẳng hàng.
– Điểm M là điểm nằm trong tam giác, điểm N là điểm nằm ngoài tam giác.
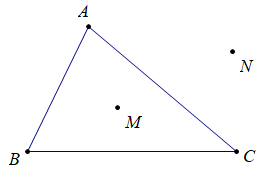
– Ba cạnh: AB, BC, CA
– Ba góc: ![]()
![]()
![]()
Bài tập tự giải
Bài tập đường tròn
Bài 1: Trên hình bên, ta có đường tròn (O; R)
| A. Điểm O cách mọi điểm trên đường tròn một khoảng R. B. Điểm O cách mọi điểm trên hình tròn một khoảng R. C. Điểm O nằm trên đường tròn D. Chỉ có câu C đúng. | 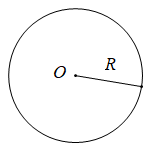 |
Bài 2: Cho ![]()
a) Những điểm cách A một khoảng 1,5cm thì nằm ở đâu? Những điểm cách B một khoảng 2cm thì nằm ở đâu?
b) Có điểm nào vừa cách A là 1,5cm; vừa cách B là 2cm không?
Bài 3: Cho đoạn thẳng AB = 3cm
a) Vẽ đường tròn (A; 1,5cm) và đường tròn (B; 1cm). Hỏi có điểm nào vừa cách A là 1,5cm; vừa cách B một khoảng 1cm;
b) Hãy nêu bước vẽ điểm M vừa cách A là 3cm, vừa cách B là 3cm.
Bài 4: Cho đoạn thẳng AB = 4cm. Hãy dựng đường tròn tâm O nhận AB làm đường kính.
Bài 5: Cho AB = 3cm, vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm), hai đường tròn này cắt nhau tại 2 điểm C, D
a) Tính độ dài đoạn thẳng CA, CB, DA, DB;
b) Tại sao đường tròn (B; 1,5cm) lại cắt đoạn thẳng AB tại trung điểm I của AB?
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính độ dài KB.
Bài 6: Vẽ đường tròn tâm O bán kính 2cm. Gọi M là một điểm nằm ngoài đường tròn tâm O; OM cắt đường tròn (O; 2cm) ở I, biết OM = 3cm.
a) Tính IM
b) Vẽ đường tròn tâm I bán kính IM. Chứng tỏ điểm O nằm ngoài đường tròn (I; IM)
c) Đường tròn (I; IM) cắt đường tròn (O; 2cm) ở P và Q, cắt OM ở K. Chứng tỏ rằng điểm K nằm trong đường tròn (O; 2cm).
Bài 7: Cho hai điểm A, B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại hai điểm C và D.
a) Tính CA và DB.
b) Tại sao (B; 1,5cm) cắt đoạn thẳng AB tại trung điểm I của AB.
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính KB.
Bài 8: Cho đoạn thẳng AB = 6cm. Vẽ đường tròn (A; 5cm) và đường tròn (B; 3cm). Hai đường tròn này cắt nhau tại M và N, các đường tròn tâm A và B theo thứ tự cắt đoạn thẳng AB tại C và D
a) Tính AM, BM
b) Chứng minh rằng D là trung điểm của đoạn AB
c) Tính độ dài CD
Bài 9: Vẽ đường tròn ![]() .
.
a) Lấy ba điểm A, B, C sao cho ![]() trong đó OA, OB là hai tia đối của nhau trên đường tròn. Hãy xác định vị trí của ba điểm trên đường tròn.
trong đó OA, OB là hai tia đối của nhau trên đường tròn. Hãy xác định vị trí của ba điểm trên đường tròn.
b) Trên hình vẽ có bao nhiêu dây cung, dây cung nòa lớn nhất. Hãy kể tên
c) Lấy điểm D và E sao cho OD = 1,5cm, OE = 3cm. Hãy xác định vị trí của điểm D và E đối với đường tròn tâm O bán kính bằng 2 cm.
Bài 10: Vẽ đường tròn (O; 2cm);
a) Lấy điểm A bất kì trên đường tròn (O; 2cm), vẽ đường tròn (A; 2cm ), đường tròn này cắt đường tròn tâm O ở trên tại 2 điểm C, D;
b) Vẽ đường tròn (C; 2cm);
c) Chứng tỏ rằng đường tròn (C; 2cm) đi qua 2 điểm O, A.
DẠNG 2: TAM GIÁC
Bài 11: Vẽ tam giác ABC có:
a) ![]()
b) ![]() ; góc
; góc ![]() ; góc
; góc ![]()
c) Góc ![]() .
.
Bài 12: Vẽ đoạn thẳng ![]() vẽ điểm F sao cho
vẽ điểm F sao cho ![]() và
và ![]() Vẽ tam giác EDF. Nói rõ cách vẽ.
Vẽ tam giác EDF. Nói rõ cách vẽ.
Bài 13: Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Cứ qua ba điểm vẽ một tam giác. Hỏi vẽ được mấy tam giác, là những tam giác nào?
Bài 14: Cho ![]() . Hãy vẽ một đường thẳng d sao cho:
. Hãy vẽ một đường thẳng d sao cho:
a) d không cắt một cạnh nào của tam giác?
b) d cắt cả ba cạnh của tam giác
Bài 15: Cho ![]() . Hãy vẽ một đường thẳng d không đi qua các đỉnh của một tam giác sao cho cắt cả ba tia AB, BC, CA.
. Hãy vẽ một đường thẳng d không đi qua các đỉnh của một tam giác sao cho cắt cả ba tia AB, BC, CA.
Bài 16: Vẽ đoạn thẳng IK sao cho ![]() Vẽ hai đường tròn
Vẽ hai đường tròn ![]() và
và ![]() chúng cắt nhau tại A và B.
chúng cắt nhau tại A và B.
a) Vẽ ![]() và
và ![]()
b) Giả sử chu vi ![]() là 8cm. Hãy tính chu vi
là 8cm. Hãy tính chu vi ![]() và tính IK.
và tính IK.
Bài 17: Cho tam giác ABC có ![]() , trên cạnh AC lấy điểm D (D không trùng với A và C).
, trên cạnh AC lấy điểm D (D không trùng với A và C).
a) Tính độ dài AC, biết AD = 4cm, CD = 3cm.
b) Tính số đo của ![]() biết
biết ![]()
c) Từ B dựng tia Bx sao cho ![]() Tính số đo
Tính số đo ![]()
d) Trên cạnh AB lấy điểm E (E không trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Bài 18: Vẽ ΔABC. Lấy M là điểm trong của ΔABC. Vẽ các tia AM, BM, CM cắt các cạnh của ΔABC tương ứng tại các điểm N, P, Q. Vẽ ΔNPQ. Hỏi điểm M có nằm trong ΔNPQ hay không?
Bài 19: Vẽ hình để thấy được mỗi câu sau đây là sai
a) Hình gồm 3 đoạn thẳng được gọi là tam giác
b) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.
c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.
d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.
e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.
f) Một điểm không thuộc cạnh của tam giác ABC thì phải nằm trong tam giác đó.
g) Một điểm không phải là đỉnh của tam giác ABC thì phải nằm trong tam giác đó.
h) Một điểm không nằm bên trong tam giác ABC thì phải nằm ngoài tam giác đó.
i) Hình gồm 2 góc được gọi là tam giác.
j) Hình gồm 3 góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được gọi là tam giác.
Hình học 6 - Tags: dây cung, đường tròn, hình tròn, tam giác, toán 6Cách chứng minh tia Oy là tia phân giác của góc xOz
Bài tập: Tia nằm giữa hai tia (xOy + yOz = xOz) – Hình học 6
Bài tập ôn chương 1 – Hình học 6
Bài tập: Điểm, đường thẳng, đoạn thẳng, tia, trung điểm đoạn thẳng
Cách chứng minh một điểm nằm giữa hai điểm – Hình học 6
Đề cương ôn thi cuối HK1 Toán lớp 6 phần Hình học
Cộng số đo góc, góc kề nhau, góc phụ nhau, góc bù nhau
