Bất phương trình bậc nhất một ẩn và cách giải

Khái niệm bất phương trình bậc nhất một ẩn, các dạng bất PT bậc nhất một ẩn và các dạng bài tập có lời giải.

Trước tiên các em ôn lại kiến thức lý thuyết bất phương bậc nhất một ẩn và các định lý.

1. Khái niệm bất phương trình bậc nhất một ẩn

Bất phương trình bậc nhất một ẩn là bất phương trình có dạng: ax + b > 0 ( hoặc ax + b < 0: ax + b ; ax + b ) trong đó x là ẩn a, b là các số đã cho a .

2. Bất phương trình tương đương

Hai bất phương trình được gọi à tương đương nếu chúng có cùng một tập hợp nghiệm.

+ Định lí 1: Nếu cộng cùng một đa thức của ẩn vào hai vế của một bất phương trình thì được một bất phương trình mới tương đương.

Hệ quả 1: Nếu xóa hai hạng tử giống nhau ở hai vế của một bất phương trình thì được một bất phương trình tương đương.
Hệ quả 2: Nếu chuyển hạng tử từ vế này sang vế kia và đổi dấu của nó thì được một bất phương trình tương đương.

+ Định lí 2:

– Nếu nhân hai vế của một bất phương trình với một số dương thì được một bất phương trình tuơng đương.

– Nếu nhân hai vế của một bất phương trình với một số âm và đổi chiều của bất phương trình thì được một bất phương đương

3. Bài tập bất phương trình bậc nhất một ẩn

Dạng 1: Giải bất phương trình bậc nhất một ẩn

Bài 1: Giải các bất phương trình sau.

a) x – 4 < – 8 b ) x + 3 > – 6 c ) -2x > -3x +3 d ) -4x -2 > -5x +6

Với bài tập này học sinh có thể giải rễ ràng bằng cách sử dụng các phép biến đổi tương đương.

Hướng dẫn giải

a) x – 4 < – 8 ⇔ x < -8 + 4 ⇔ x < – 4

Vậy tập nghiệm của bất phương trình đã cho là: $\displaystyle \displaystyle S=\left\{ {x\in \mathbb{R}\text{ }\!\!|\!\!\text{ }x<-4\text{ }} \right\}$

b ) x + 3 > – 6 ⇔ x > – 6 – 3 ⇔ x > -9

Vậy tập nghiệm của bất phương trình đã cho là: $\displaystyle \displaystyle S=\left\{ {x\in \mathbb{R}\text{ }\!\!|\!\!\text{ }x>-9\text{ }} \right\}$

c) -2x > – 3x + 3 ⇔ -2x + 3x > 3 ⇔ x > 3

Vậy tập nghiệm của bất phương trình đã cho là:

d) – 4x – 2.> -5x + 6 ⇔ – 4x + 5x > 6 + 2 ⇔ x > 8

Vậy bất phương trình đã cho có nghiệm là: $\displaystyle \displaystyle S=\left\{ {x\in \mathbb{R}\text{ }\!\!|\!\!\text{ }x>8} \right\}$

Bài 2: Giải các bất phương trình sau ;

a ) (x + 2 ) ² < 2x ( x + 2) +4 b ) (x + 2 ) ( x + 4 ) > ( x – 2 ) (x + 8) + 26

Bài tập này sẽ làm cho học sinh hơi bối rối vì các em thấy lũy thừa của x không là bậc nhất nên không biết làm như thế nào vì vậy giáo viên đưa ra một gợi ý nhỏ cho các em: Hãy thực hiện các phép tính ở hai vế và thu gọn.

Hướng dẫn giải

a. ( x + 2 ) ² < 2x ( x + 2) + 4 $\displaystyle \displaystyle \Leftrightarrow$ x² + 4x + 4 < 2 x² + 4x + 4
$\displaystyle \displaystyle \Leftrightarrow$ x² < 2 x² ↔ x²> 0 $\displaystyle \displaystyle \Leftrightarrow$ x > 0 hoặc x < 0.

Sau khi giải đến bất phương trình x²> 0 sẽ có nhiều học sinh biến đổi như sau; x²> 0 ↔ x > 0 như vậy thì khi kết luận nghiệm thì sẽ thiếu nghiệm của bất phương trình vì vậy cần nhắc lại cho các em lũy thừa chẵn của một số, biểu thức bao giờ cũng lớn hơn hoặc bằng 0 do vậy thay cho việc tìm các gía trị của x để x² > 0 ta đưa về tìm x để x² = 0 khi đó những giá trị còn lại của x sẽ làm cho x² > 0.

b ) ( x + 2) ( x + 4 ) > ( x – 2 ) ( x + 8 ) + 26

↔ x² + 6x + 8 > x² + 6x -16 + 26 ↔0 > 2 ( vô lí )

Nên: Bất phương trình vô nghiệm.

Khi làm xong bài tập 2 giáo viên có thể cho học sinh rút ra các bước làm:

Bước 1: Thực hiện các phép tính ở hai vế của bất phương trình.

Bước 2: Chuyển các hạng tử chứa ẩn sang một vế, các hạng tử bằng số sang một vế rồi thu gọn bất phương trình

Bước 3: Giải bất phương trình sau khi thu gọn.

Dạng 2: Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối

Với dạng toán này để giải bất phương trình loại này ta phải khử dấu giá trị tuyệt đối. Ta nhớ lại rằng: Giá trị tuyệt đối của một biểu thức bằng chính nó nếu biểu thức không âm, bằng số đối của nó nếu biểu thức âm.

$\displaystyle \left| A \right|=\left\{ \begin{array}{l}A\,\,\,khi\,\,A\ge 0\\-A\,khi\,A<0\end{array} \right.$

Do đó để khử dấu giá trị tuyệt đối cần xét giá trị của biến làm cho biểu thức âm hay không âm. Nếu biểu thức nằm trong dấu giá trị tuyệt đối là nhị thức bậc nhất ta cần nhớ định lí sau:

Định lí về dấu của nhị thức bậc nhất ax + b ( a ≠ 0 )

Nhị thức ax + b ( a ≠ 0 )

+ Cùng dấu với a với các giá trị của x lớn hơn nghiệm của nhị thức.

+ Trái dấu với a với các giá trị của x nhỏ hơn nghiệm của nhị thức.

Bài 1: Giải các bất phương trình sau

a) │3x – 1│ > 5 b) │3-2x│ < x + 1

Hướng dẫn giải

a) $\displaystyle$ │3x – 1│ > 5 ( 1 )

* Xét khoảng x < $\displaystyle \frac{1}{3}$ thì ( 1) có dạng 1 – 3x > 5 ⇔ -3x>5-1 \displaystyle \Leftrightarrow -3x>4\Leftrightarrow x<\frac{{-4}}{3} $Nghiệm của bất phương trình trong khoảng này là x <$ \displaystyle \frac{{-4}}{3} $* Xét khoảng$ \displaystyle x\ge \frac{1}{3} $thì (1) có dạng$ \displaystyle 3x-1>5\Leftrightarrow 3x>5+1\Leftrightarrow 3x>6\Leftrightarrow x>2 $Nghiệm của bất phương trình trong khoảng này là x > 2 Kết luận: Nghiệm của bất phương trình đã cho là: x > 2: x <$ \displaystyle \frac{{-4}}{3} $b)$ \displaystyle $│3-2x│ < x + 1 * Xét khoảng x >$ \displaystyle \frac{3}{2} $,(2) có dạng$ \displaystyle 2x-3<x+1\Leftrightarrow 2x-x<3+1\Leftrightarrow x<4 $Vậy bất phương trình có nghiệm trong khoảng này là$ \displaystyle \frac{3}{2}<x<4 $* Xét khoảng$ \displaystyle x\le \frac{3}{2} $, ( 2 ) có dạng$ \displaystyle 3-2x<x+1\Leftrightarrow -2x-x<1-3\Leftrightarrow -3x<-2\Leftrightarrow x>\frac{2}{3} $Vậy bất phương trình có nghiệm trong khoảng này là$ \displaystyle \frac{2}{3}<x\le \frac{3}{2} $Kết luận: Nghiệm của bất phương trình đã cho là:$ \displaystyle \frac{2}{3}<x<4 $. <span style="text-decoration: underline;"><strong>Bài 2: </strong></span>Giải bất phương trình a) │x│- x + 2 \le 2│x - 4│ (1) b) │x - 1│+│x - 5│> 8 (2) <strong>Hướng dẫn giải</strong> a) Lập bảng xét dấu các biểu thức x và x - 4 <table> <tbody> <tr> <td width="163">x</td> <td width="478"> 0 4</td> </tr> <tr> <td width="163">x</td> <td width="478"> - 0 + │ +</td> </tr> <tr> <td width="163">x - 4</td> <td width="478"> - │ - 0 +</td> </tr> </tbody> </table> * Xét khoảng x < 0; ( 1) có dạng - x - x + 2 \le 2 ( 4 - x )$ \displaystyle \Leftrightarrow 0x=6 $Nghiệm đúng với mọi x thuộc khoảng đang xét x < 0 * Xét khoảng 0 \le x < 4 ,(1) có dạng x - x + 2 \le 8 - 2x$ \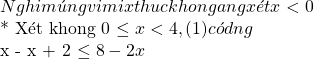displaystyle \Leftrightarrow x\le 3 $Nghiệm của bất phương trình đang xét trong khoảng này là 0 \le x \le 3 * Xét khoảng x \ge 4, (1) có dạng x - x + 2 \le 2x - 8 ↔ x \ge 5 thỏa mãn x \ge 4 Kết luận: Nghiệm của bất phương trình đã cho là x \le 3; x \ge 5 b) Lập bảng xét dấu các biểu thức ( x - 1 ); ( x - 5 ) <table> <tbody> <tr> <td width="163">x</td> <td width="478"> 1 5</td> </tr> <tr> <td width="163">x - 1</td> <td width="478"> - 0 + │ +</td> </tr> <tr> <td width="163">x - 5</td> <td width="478"> - │ - 0 +</td> </tr> </tbody> </table> * Xét khoảng x < 1, (2) có dạng$ \displaystyle 1-x+5-x>8\Leftrightarrow -2x>2\Leftrightarrow x<-1 $thỏa mãn x < 1 * Xét khoảng 1 \le x < 5, (2) có dạng$ \displaystyle x-1+5-x>8\Leftrightarrow 0x>2 $không xảy ra với mọi x do đó bất phương trình vô nghiệm trong khoảng đang xét. * Xét khoảng x \ge 5, ( 2) có dạng$ \displaystyle x-1+x-5>8\Leftrightarrow 2x>14\Leftrightarrow x>7 $nghiệm đúng với mọi x \ge 5 <strong>Kết luận:</strong> Nghiệm của bất phương trình đã cho là x < - 1; x > 7. <strong>Nhận xét:</strong> Trong cách cách giải trên ta đã khử dấu GTTĐ bằng cách xét từng khoảng giá trị của biến. Trong một số trường hợp, có thể giải nhanh hơn cách dùng phương pháp chung nói trên bởi các biến đổi tương đương sau: <strong>Dạng 1:</strong> a) Với a là số dương, ta có: │f(x) │ < a$ \displaystyle \Leftrightarrow -a<f(x)<a $b) │f(x) │ < g (x)$ \displaystyle \Leftrightarrow -g(x)<f(x)<g(x) $<strong>Dạng 2: </strong> a) Với số a dương ta có: │f(x) │ > a$ \displaystyle \displaystyle \Leftrightarrow \left[ \begin{array}{l}f(x)<-a\\f(x)>a\end{array} \right. $b) │f(x) │ > g (x)$ \displaystyle \Leftrightarrow \left[ \begin{array}{l}f(x)<-g(x)\\f(x)>g(x)\end{array} \right. $<strong>Dạng 3:</strong> │f(x)│ > │g(x)│$ \displaystyle \Leftrightarrow {{\left[ {f(x)} \right]}^{2}}>{{\left[ {g(x)} \right]}^{2}} $<h4>Dạng 3: Bất phương trình tích, bất phương trình thương</h4> Với dạng bài tập này học sinh có thể lập bảng để xét dấu nhưng cũng có thể sử dụng các phép biến đổi tương đương. Khi sử dụng phép biến đổi tương đương cần chú ý: - Tích (thương ) của hai số cùng dấu là số dương - Tích ( thương ) của hai số trái dấu là số âm. 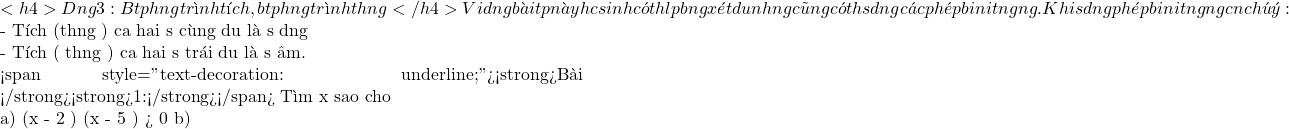<span style="text-decoration: underline;"><strong>Bài </strong><strong>1:</strong></span> Tìm x sao cho a) (x - 2 ) (x - 5 ) > 0 b)$ \displaystyle \frac{{x+2}}{{x-5}} $< 0 <strong>Hướng dẫn giải</strong> a) <strong>Cách 1</strong>: lập bảng xét dấu x - 2 và x - 5 <table> <tbody> <tr> <td width="175">x</td> <td width="466"> 2 5</td> </tr> <tr> <td width="175">x - 2</td> <td width="466"> - 0 + │ +</td> </tr> <tr> <td width="175">x - 5</td> <td width="466"> - │ - 0 +</td> </tr> <tr> <td width="175">(x - 2) ( x - 5 )</td> <td width="466"> + 0 - 0 +</td> </tr> </tbody> </table> <strong>Kết luận:</strong> Nghiệm của bất phương trình là x < 2 hoặc x > 5 <strong>Cách 2:</strong> Sử dụng phép biến đổi tương đương. ( x - 2 ) ( x - 5 ) > 0$ \displaystyle \left[ \begin{array}{l}\left\{ \begin{array}{l}x-2>0\\x-5>0\end{array} \right.\\\left\{ \begin{array}{l}x-2<0\\x-5<0\end{array} \right.\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x>2\\x>5\end{array} \right.\\\left\{ \begin{array}{l}x<2\\x<5\end{array} \right.\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}x>5\\x<2\end{array} \right. $Kết luận: Nghiệm của bất phương trình là: x > 5; x < 2 c. Lập bảng xét dấu của các nhị thức <table> <tbody> <tr> <td width="151">x</td> <td width="490"> -2 5</td> </tr> <tr> <td width="151">x + 2</td> <td width="490"> - 0 + │ +</td> </tr> <tr> <td width="151">x - 5</td> <td width="490"> - │ - 0 +</td> </tr> <tr> <td width="151"></td> <td width="490"> + 0 - ║ +</td> </tr> </tbody> </table> Kết luận: Nghiệm của bất phương trình là x < -2; x > 5. <span style="text-decoration: underline;"><strong>Bài </strong><strong>2:</strong></span> Giải các bất phương trình sau a. x<sup>2</sup> - 2x + 1 < 9 b. ( x<sup>3</sup> -27) ( x<sup>3</sup> - 1 ) ( 2x + 3 - x<sup>2</sup>) \ge 0 <strong>Hướng dẫn giải</strong> a) Cách 1: x<sup>2</sup> - 2x + 1 < 9$ \displaystyle \Leftrightarrow {{(x-1)}^{2}}<9\Leftrightarrow \left| {x-1} \right|<9 \displaystyle \Leftrightarrow -3<x-1<3\Leftrightarrow -2<x<4 $Cách 2: Biến đổi bất phương trình về dang bất phương trình tích$ \displaystyle \begin{array}{l}{{x}^{2}}-2x+1<9\Leftrightarrow {{x}^{2}}-2x-8<0\\\Leftrightarrow \left( {x+2} \right)\left( {x-4} \right)<0\end{array} $Lập bảng xét dấu của nhị thức (x + 2 ), ( x - 4 ) <table> <tbody> <tr> <td width="175">x</td> <td width="466"> -2 4</td> </tr> <tr> <td width="175">x + 2</td> <td width="466"> - 0 + │ +</td> </tr> <tr> <td width="175">x - 4</td> <td width="466"> - │ - 0 +</td> </tr> <tr> <td width="175">(x + 2) ( x - 4 )</td> <td width="466"> + 0 - 0 +</td> </tr> </tbody> </table> Nghiệm của bất phương trình là - 2 < x < 4 b. 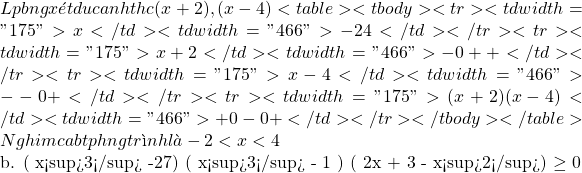( x<sup>3</sup> -27) ( x<sup>3</sup> - 1 ) ( 2x + 3 - x<sup>2</sup>) \ge 0$ \displaystyle \begin{array}{l}\Leftrightarrow \left( {x-3} \right)\left( {{{x}^{2}}+3x+9} \right)\left( {x+1} \right)\left( {{{x}^{2}}-x+1} \right)\left( {3-x} \right)\left( {x+1} \right)\ge 0\\\Leftrightarrow \left( {x-3} \right){{\left( {x+1} \right)}^{2}}\left( {3-x} \right)\ge 0\Leftrightarrow -{{\left( {x-3} \right)}^{2}}{{\left( {x+1} \right)}^{2}}\ge 0\Leftrightarrow \left[ \begin{array}{l}x=3\\x=-1\end{array} \right.\end{array}$

Vậy nghiệm của bất phương trình là x = 3, x = – 1.

Đại số 8 - Tags: bất phương trình, toán 8