Cách chứng minh 2 đường thẳng song song trong không gian

Phương pháp chứng minh 2 đường thẳng song song trong không gian bằng 3 cách. Áp dụng vào giải bài tập chứng minh hai đường thẳng song song.

*Định nghĩa:

Hai đường thẳng song song nếu chúng đồng phẳng và không có điểm chung.

Cách chứng minh hai đường thẳng song song

Các em có thể dùng 3 cách dưới đây:

– Cách thứ nhất: Chứng minh chúng đồng phẳng rồi sử dụng các định lí đường trung bình, Thales đảo … quen thuộc trong hình học phẳng.

– Cách thứ hai: Chứng minh chúng cùng song song với đường thẳng thứ ba.

– Cách thứ ba: Dùng hệ quả: Nếu hai mặt phẳng cắt nhau lần lượt chứa hai đường thẳng song song thì giao tuyến (nếu có) của chúng song song hoặc trùng với một trong hai đường thẳng đó.

Ví dụ có lời giải

Đọc 5 ví dụ dưới đây để biết cách chứng minh 2 đường thẳng song song trong không gian như thế nào nhé.

Ví dụ 1: Cho tứ diện ABCD .Gọi I ,J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh  : IJ ∕ ∕ CD

Ví dụ giải

Cách chứng minh 2 đường thẳng song song trong không gian

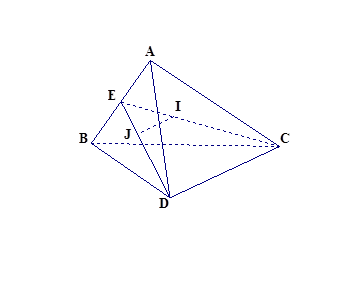
Gọi E là trung điểm của AB. theo tính chất trọng tâm ta có tỉ số  EJ/ED = EI/EC = 1/3 ( Tính chất trọng tâm)

⇒ IJ // CD ( Định lí talet đảo )

Ví dụ 2: Cho hình chóp S.ABCD với  đáy ABCD là hình bình hành .Gọi A’ ,B’ , C’ ,D’ lần lượt là trung điểm các cạnh SA , SB , SC , SD

a. Chứng minh A’B’C’D’ là hình bình hành

b. Gọi M là điểm bất kì trên BC . Tìm thiết diện của (A’B’M) với hình chóp S.ABCD

Ví dụ giải

Cách chứng minh 2 đường thẳng song song trong không gian

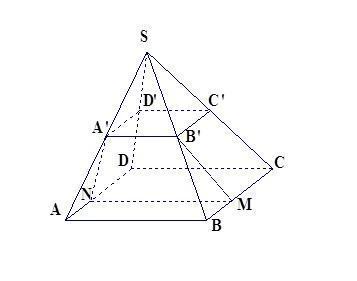
Chứng minh A’B’C’D’ là hình bình hành :

Trong tam giác SAB, ta có : A’B’ // AB

Trong tam giác SCD, ta có C’D’//CD  Mặt   khác AB // CD    ⇒  A’B’  // C’D’

Vậy : A’B’C’D’ là hình bình hành

Tìm thiết diện của (A’B’M) với hình chóp S.ABCD:

Ta  có : AB  ∕ ∕  A’B’ và  M  là điểm chung của (A’B’M) và (ABCD)

Do đó giao tuyến của (A’B’M) và (ABCD) là  Mx  song song   AB và A’B’. Gọi   N = Mx ∩ AD

Vậy :  thiết diện là hình thang A’B’MN

 Bài 3: 

Cho hình chóp S.ABCD với  đáy ABCD là hình thang với cạnh đáy AB  và CD (AB >CD).  Gọi M , N  lần lượt là trung  điểm các cạnh SA , SB

a. Chứng minh : MN ∕ ∕ CD

b. Tìm P = SC ∩ (ADN)

c. Kéo dài AN và DP cắt nhau tại I.  Chứng minh : SI  ∕ ∕ AB  ∕ ∕ CD . Tứ giác SABI là hình gì ?

Ví dụ giải

Cách chứng minh 2 đường thẳng song song trong không gian

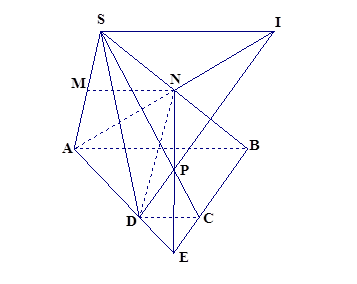
Chứng minh : MN ∕ ∕ CD :

Trong tam giác SAB, ta có : MN  ∕ ∕ AB

Mà   AB  ∕ ∕  CD  ( ABCD là hình thang )

Vậy : MN ∕ ∕  CD

Tìm P = SC ∩ (ADN):

Ta có :  N là điểm chung của (SBC ) và (ADN)

Trong (ABCD), gọi  E = AD ∩ AC

⇒ ( SBC) ∩ (ADN ) = NE

Vậy : P  = SC ∩ ( ADN )

Chứng minh : SI // AB //  CD . Tứ giác SABI là hình gì ?

SI = (SAB) ∩(SCD)

AB // CD

⇒ SI // AB // CD (1)

Trong tam giác SAI có SI // MN , SI = 2MN  và AB = 2 MN ⇒ SI = AB (2)

Từ (1) và (2) ⇒ SABI là hình bình hành

Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang (đáy lớn AB). Gọi I, J lần lượt là trung điểm  AD và BC , K là điểm trên  cạnh SB sao cho SK = 2/3SB .

a. Tìm giao tuyến của (SAB) và (IJK)

b. Tìm thiết diện của (IJK) với hình chóp S.ABCD. Tìm điều kiện để thiết diện là hình bình hành

Ví dụ giải

Cách chứng minh 2 đường thẳng song song trong không gian

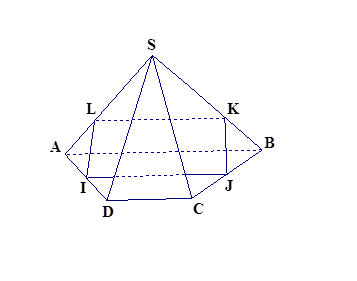
Tìm giao tuyến của (SAB) và (IJK):

Ta  có : AB  ∕ ∕  IJ và  K  là điểm chung của (SAB) và (IJK)  Vậy : giao tuyến là đường thẳng Kx  song song AB

Tìm thiết diện của (IJK) với hình chóp S.ABCD :

Gọi   L = Kx ∩ SA

Thiết diện  là hình thang  IJKL

Do : IJ là đường trung bình của hình thang ABCD ⇒ IJ = 1/2 (AB + CD)

Xét  tam giác SAB có :  LK/AB = SK/SB = 2/3   ⇒  LK =2/3.AB

IJKL là hình bình hành ⇔ IJ  =  KL ⇔ 1/2.(AB + CD)  = 2/3.AB ⇔ AB  = 3.CD

Vậy : thiết diện IJKL  là hình bình hành  ⇔ AB  =  3.CD

Ví dụ 5: Cho hình chóp S.ABCD có  đáy ABCD là hình bình hành. Gọi M ,N ,P , Q  lần lượt là các điểm nằm trên   các cạnh  BC , SC , SD ,AD sao  cho MN // BS , NP // CD , MQ // CD

a. Chứng minh : PQ // SA.

b. Gọi  K =  MN ∩ PQ. Chứng minh điểm K nằm trên đường thẳng cố định khi M di động trên cạnh BC.

Ví dụ giải

Cách chứng minh 2 đường thẳng song song trong không gian

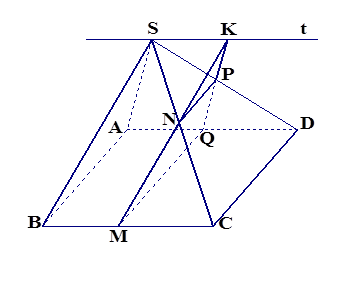
Chứng minh : PQ // SA.

Xét tam giác SCD.  Ta có : NP // CD  ⇔    DP/SD = CN/CS (1)

tương tự MN // SB ta có CN /CS = CM/CB (2)

Ta có MQ // AB ⇒ CM / CB = DQ/ DA (3)

từ (1), (2) và (3) ⇒ DP / DS = DQ / DA ⇒ PQ // SA

Hình học 11 - Tags: , , ,