Cách chứng minh 2 hai điểm trùng nhau bằng vectơ
Phương pháp chung
Muốn chứng minh 2 điểm ![]() và
và ![]() trùng nhau, chúng ta có thể sử dụng một trong hai cách sau:
trùng nhau, chúng ta có thể sử dụng một trong hai cách sau:
– Cách 1: Chứng minh cho ![]() .
.
– Cách 2: Chứng minh cho ![]() với O là điểm tùy ý.
với O là điểm tùy ý.
Ứng dụng vectơ chứng minh 2 điểm trùng nhau
Bài toán: Cho tứ giác lồi ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng hai tam giác ANP và CMQ có cùng trọng tâm.
Giải
Gọi ![]() lần lượt là trọng tâm của tam giác ANP và CMQ và O là một điểm tùy ý.
lần lượt là trọng tâm của tam giác ANP và CMQ và O là một điểm tùy ý.
Ta có:
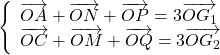
Mặt khác:
![]()
![]() (2)
(2)
![]()
![]() (3)
(3)
Từ (1), (2), (3) suy ra: ![]()
Vậy ![]() và
và ![]() trùng nhau.
trùng nhau.
Bài tập
Bài 1: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Bài 2: Cho lục giác ABCDEF có ![]() và hai tam giác ACE và BDF có cùng trọng tâm. CMR: AB²+EF²=CD².
và hai tam giác ACE và BDF có cùng trọng tâm. CMR: AB²+EF²=CD².
