Cách giải hệ phương trình bậc nhất hai ẩn số
Để giải hệ phương trình bậc nhất hai ẩn số chúng ta thường dùng một trong các cách: thế, cộng đại số, đặt ẩn phụ.
Nhắc lại lý thuyết: Định nghĩa về hệ phương trình bậc nhất hai ẩn số.
+ Hệ phương trình bậc nhất hai ẩn có dạng ![]()
Trong đó a, b, a’ và b’ không đồng thời bằng 0.
Phương pháp giải hệ phương trình bậc nhất hai ẩn số
a. Phương pháp thế
+ Dùng quy tắc thế biến đổi hệ phương trình đã cho thành một hệ mới trong đó có phương trình một ẩn
+ Giải phương trình một ẩn này rồi duy ra nghiệm của hệ
Ví dụ: Giải hệ phương trình bằng phương pháp thế:
![]()
![]()
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) = (2;1)
b. Phương pháp cộng đại số
+ Nhân hai vế của mỗi phương trình với một thừa số phụ sao cho giá trị tuyệt đối của hệ số của một ẩn nào đó trong hai phương trình bằng nhau
+ Dùng quy tắc cộng đại số để được một hệ mứi trong đó có một phương trình một ẩn
+ Giải phương trình một ẩn này rồi suy ra nghiệm của hệ
Ví dụ: Giải hệ phương trình bằng phương pháp cộng đại số:
![]()
![]()
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) = (2;1)
c. Phương trình bằng cách đặt ẩn phụ
+ Bước 1: Đặt điều kiện để hệ có nghĩa
+ Bước 2: Đặt ẩn phụ và điều kiện của ẩn phụ
+ Bước 3: Giải hệ theo các ẩn phụ đã đặt (sử dụng phương pháp thế hoặc phương pháp cộng đại số)
+ Bước 4: Trở lại ẩn ban đầu để tìm nghiệm của hệ
Ví dụ: Giải hệ phương trình bằng phương pháp đặt ẩn phụ:
Giải hệ phương trình: 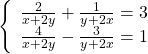
Điều kiện ![]()
Đặt ![]()
Hệ phương trình đã cho trở thành:
![]()
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) = (1;1)
Bài tập giải hệ phương trình bậc nhất 2 ẩn
Bài 1: Giải các hệ phương trình sau:
1) ![]()
2)![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
Bài 2: Giải các hệ phương trình sau:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
Bài 3: Giải các hệ phương trình sau:
1) 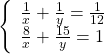
2) 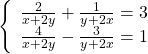
3) 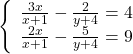
4) ![]()
5) ![]() 6)
6)![]()
7) ![]()
8) ![]()
68 bài tập: giải toán bằng cách lập phương trình, hệ phương trình
Chuyên đề: Phương trình và hệ phương trình ôn thi vào 10
Bài tập Đại số 9 chương 2: Hàm số bậc nhất
10 bài toán rút gọn biểu thức có lời giải
Các dạng bài tập Đại số ôn thi vào lớp 10
Phương pháp giải hệ phương trình bậc cao
Cách tìm hệ số a, b của hàm số bậc nhất y = ax + b