Cách xác định giá trị của tham số để hệ PT bậc nhất có nghiệm thỏa mãn điều kiện cho trước

Phương pháp giải

+ Giải hệ phương trình theo tham số

+ Viết x, y của hệ về dạng: \displaystyle n+\frac{k}{{f(m)}}

với n, k nguyên

+ Tìm m nguyên để f(m) là ước của k

Ví dụ có lời giải

Tìm m nguyên để hệ có nghiệm duy nhất là nghiệm nguyên: \left\{ \begin{array}{l}mx+2y=m+1\\2x+my=2m-1\end{array} \right.

\displaystyle \left\{ \begin{array}{l}mx+2y=m+1\\2x+my=2m-1\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}2mx+4y=2m+2\\2mx+{{m}^{2}}y=2{{m}^{2}}-m\end{array} \right.

\displaystyle \left\{ \begin{array}{l}\left( {{{m}^{2}}-4} \right)y=2{{m}^{2}}-3m-2=\left( {m-2} \right)\left( {2m+1} \right)\\2x+my=2m-1\end{array} \right.

để hệ có nghiệm duy nhất thì  m2 – 4 ≠ 0 hay m ≠ ±2

Vậy với m ≠ ±2 hệ phương trình có nghiệm duy nhất

\displaystyle \left\{ {\begin{array}{*{20}{l}} {y=\frac{{(m-2)(2m+1)}}{{{{m}^{2}}-4}}=\frac{{2m+1}}{{m+2}}=2-\frac{3}{{m+2}}} \\ {x=\frac{{m-1}}{{m+2}}=1-\frac{3}{{m+2}}} \end{array}} \right.

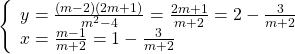
Để x, y là những số nguyên thì m + 2 ∈ Ư(3) = {1;-1;3;-3}

Vậy: m + 2 = ±1, ±3 => m = -1; -3; 1; -5 thì hệ PT đã cho có  nghiệm duy nhất là nghiệm nguyên

Bài tập

Bài 1:

Cho hệ phương trình \displaystyle \left\{ \begin{array}{l}mx+4y=10-m\\x+my=4\end{array} \right. (m là tham số)

a) Giải hệ phương trình khi \displaystyle m=\sqrt{2}

b) Giải và biện luận hệ phương trình theo m

c) Xác định các giá trị nguyên của m để hệ có nghiệm duy nhất (x;y) sao cho x> 0, y > 0

d) Với giá trị nào của m thì hệ có nghiệm (x;y) với x, y là các số nguyên dương

Bài 2:

Cho hệ phương trình: \displaystyle \left\{ \begin{array}{l}(m-1)x-my=3m-1\\2x-y=m+5\end{array} \right.

a) Giải và biện luận hệ phương trình theo m

b) Với giá trị nguyên nào của m để hai đường thẳng của hệ cắt nhau tại một điểm nằm trong góc phần tư thứ IV của hệ tọa độ Oxy

c) Định m để hệ có nghiệm duy nhất (x ; y) sao cho P = x2 + y2 đạt giá trị nhỏ nhất.

Bài 3:

Cho hệ phương trình \displaystyle \left\{ \begin{array}{l}3x+2y=4\\2x-y=m\end{array} \right.

a) Giải hệ phương trình khi m = 5

b) Tìm m nguyên sao cho hệ có nghiệm (x; y) với x < 1, y < 1

c) Với giá trị nào của m thì ba đường thẳng 3x + 2y = 4; 2x – y = m; x + 2y = 3 đồng quy

Bài 4:

Cho hệ phương trình: \displaystyle \left\{ \begin{array}{l}mx+4y=9\\x+my=8\end{array} \right.

a) Giải hệ phương trình khi m = 1

b) Với giá trị nào của m để hệ có nghiệm (-1 ; 3)

c) Với giá trị nào của m thì hệ có nghiệm duy nhất, vô nghiệm

Bài 5:

Cho hệ phương trình: \displaystyle \left\{ \begin{array}{l}x+my=9\\mx-3y=4\end{array} \right.

a) Giải hệ phương trình khi m = 3

b) Với giá trị nào của m để hệ có nghiệm (-1 ; 3)

c) Chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m

d) Với giá trị nào của m để hệ có nghiệm (x ; y) thỏa mãn hệ thức:

\displaystyle x-3y=\frac{{28}}{{{{m}^{2}}+3}}-3

Bài 6:

Cho hệ phương trình:\displaystyle \left\{ \begin{array}{l}mx-y=2\\3x+my=5\end{array} \right.

a) Giải hệ phương trình khi \displaystyle m=\sqrt{2}.

b) Tìm giá trị của m để hệ phương trình đã cho có nghiệm (x; y) thỏa mãn hệ thức \displaystyle x+y=1-\frac{{{{m}^{2}}}}{{{{m}^{2}}+3}}.

Bài 7:

Cho hệ phương trình \displaystyle \left\{ \begin{array}{l}3x-my=-9\\mx+2y=16\end{array} \right.

a) Giải hệ phương trình khi m = 5

b) Chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m

c) Định m để hệ có nghiệm (x ; y) = ( 1,4 ; 6,6)

d) Tìm giá trị nguyên của m để hai đường thẳng của hệ cắt nhau tại một điểm nằm trong góc phần tư thứ IV trên mặt phẳng tọa độ Oxy

e) Với trị nguyên nào của m để hệ có nghiệm (x ; y) thỏa mãn x + y = 7

Đại số 9 - Tags: , , ,