Chứng minh giá trị biểu thức không phụ thuộc vào biến

Cách chứng minh giá trị của biểu thức không phụ thuộc vào biến qua ví dụ minh họa có lời giải được chia sẻ bởi Gia sư Tiến Bộ.

Dạng bài tập chứng minh giá trị biểu thức không phụ thuộc vào biến được học trong chương trình Đại số lớp 8.

Thế nào là biểu thức không phụ thuộc vào biến?

Biểu thức không phụ thuộc vào biến là biểu thức sau khi rút gọn không còn chứa biến.

Cách chứng minh giá trị biểu thức không phụ thuộc vào biến:

Để chứng minh giá trị biểu thức không phụ thuộc vào biến chúng ta thực hiện biến đổi biểu thức đã cho bằng cách nhân đơn thức với đơn thức, nhân đa thức với đa thức và thu gọn kết quả.

Ví dụ: Chứng minh giá trị của biểu thức sau không phụ thuộc vào x

:

a) \displaystyle {A=x\cdot (2x+1)-{{x}^{2}}\cdot (x+2)+\left( {{{x}^{3}}-x+5} \right)}

b) \displaystyle {B=x\cdot \left( {3{{x}^{2}}-x+5} \right)-\left( {2{{x}^{3}}+3x-16} \right)-x\cdot \left( {{{x}^{2}}-x+2} \right)}

Hướng dẫn giải:

a) Biến đổi biểu thức A, ta có:

\displaystyle \begin{array}{*{20}{l}} {A=x\cdot (2x+1)-{{x}^{2}}\cdot (x+2)+\left( {{{x}^{3}}-x+5} \right)} \\ {A=2{{x}^{2}}+x-{{x}^{3}}-2{{x}^{2}}+{{x}^{3}}-x+5} \\ {A=6} \end{array}

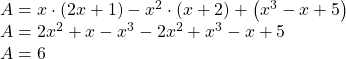
Suy ra giá trị của A không phụ thuộc vào x

.

b) Biến đổi biểu thức B, ta có:

\displaystyle \begin{array}{*{20}{l}} {B=x\cdot \left( {3{{x}^{2}}-x+5} \right)-\left( {2{{x}^{3}}+3x-16} \right)-x\cdot \left( {{{x}^{2}}-x+2} \right)} \\ {B=3{{x}^{3}}-{{x}^{2}}+5x-2{{x}^{3}}-3x+16-{{x}^{3}}+{{x}^{2}}-2x} \\ {B=3{{x}^{3}}-3{{x}^{3}}+{{x}^{2}}-{{x}^{2}}+5x-5x+16} \\ {B=16} \end{array}

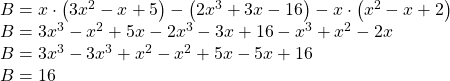
Suy ra giá trị của B không phụ thuộc vào x

.

Bài tập chứng minh giá trị biểu thức không phụ thuộc vào biến:

Bài 1: Chứng tỏ rằng mỗi biểu thức sau không phụ thuộc vào giá trị của biến x

.

A=\left( {{{x}^{2}}-2} \right)\left( {{{x}^{2}}+x-1} \right)-x\left( {{{x}^{3}}+{{x}^{2}}-3x-2} \right);

B=2\left( {2x+{{x}^{2}}} \right)-{{x}^{2}}\left( {x+2} \right)+\left( {{{x}^{3}}-4x+3} \right).

Bài 2: Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.

a) x(5 x-3)-x^{2}(x-1)+x\left(x^{2}-6 x\right)-10+3 x

b) x\left(x^{2}+x+1\right)-x^{2}(x+1)-x+5

c) (x-5)(2 x+3)-2 x(x-3)+x+7

Đại số 8 - Tags: , ,