Đề thi khảo sát Toán 9 lần 1 THCS Nguyễn Văn Huyên 2020-2021

Đề thi khảo sát Toán 9 lần 1 trường THCS Nguyễn Văn Huyên, huyện Hoài Đức, thành phố Hà Nội, năm học 2020-2021.

Thời gian làm bài 120 phút. Hình thức thi tự luận gồm 5 bài.

Đề thi khảo sát Toán 9 lần 1 THCS Nguyễn Văn Huyên 2020-2021

Đáp án Bài 5: Cho các số dương a và b thỏa mãn a + b ≤ 1. Tìm giá trị nhỏ nhất của biểu thức:

\displaystyle P=\dfrac{1}{{a^{2}+b^{2}}}+\dfrac{1}{{ab}}+4ab

Giải:

Áp dụng BĐT phụ: \displaystyle a^{2}+b^{2}\ge \dfrac{{{(a+b)}^{2}}}{2};(a+b)^{2}\ge 4ab

\displaystyle P=\dfrac{1}{{a^{2}+b^{2}}}+\dfrac{1}{{ab}}+4ab\ge \dfrac{1}{{{(a+b)}^{2}}}+\left( {\dfrac{1}{{4ab}}+4ab} \right)+\dfrac{3}{{4ab}}

Vì a + b ≤ 1, áp dụng bất đẳng thức Cosi cho 2 số dương \displaystyle {\dfrac{1}{{4ab}}} và \displaystyle {4ab}.

\displaystyle P\ge \dfrac{2}{{{(a+b)}^{2}}}+2\sqrt{{\dfrac{1}{{4ab}}\cdot 4ab}}+\dfrac{3}{{{(a+b)}^{2}}}\ge \dfrac{2}{{1^{2}}}+2+\dfrac{3}{{1^{2}}}=7

Dấu “=” xảy ra ⇔ 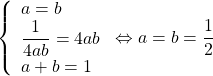\displaystyle \left\{ {\begin{array}{*{20}{l}} {a=b} \\ {\dfrac{1}{{4ab}}=4ab} \\ {a+b=1} \end{array}} \right.\Leftrightarrow a=b=\dfrac{1}{2}

Vậy giá trị nhỏ nhất của P là 7.

Đề thi Toán lớp 9 - Tags: ,