Cách chứng minh tứ giác là hình bình hành – Toán 8
Hướng dẫn học sinh lớp 8 cách chứng minh tứ giác là hình bình hành qua các dấu hiệu nhận biết và ví dụ có lời giải.
Muốn làm được các bài toán chứng minh hình học thì chúng ta phải nắm vững khái niệm, tính chất và chứng minh một tứ giác là hình bình hành cũng vậy.
1. Định nghĩa hình bình hành
Hình bình hành là tứ giác có các cặp cạnh đối song song.
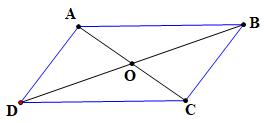
Hình bình hành ABCD
Theo định nghĩa: tứ giác ABCD là hình bình hành ⇔ AB // CD và AD // BC.
2. Tính chất hình bình hành
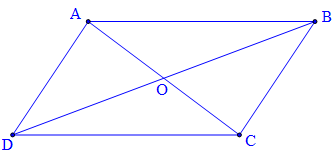
Hình bình hành ABCD
Trong hình bình hành ABCD có:
• Các cạnh đối bằng nhau: AB = CD và AD = BC.
• Các góc đối bằng nhau: góc A = góc C, góc B = góc D.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC và OB = OD.
3. Dấu hiệu nhận biết hình bình hành
• Tứ giác có các cạnh đối song song là hình bình hành.
• Tứ giác có các cạnh đối bằng nhau là hình bình hành.
• Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Cách chứng minh tứ giác là hình bình hành
Để chứng minh tứ giác là hình bình hành chúng ta dựa vào Định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành đã học. Cụ thể là những cách sau:
Chứng minh tứ giác có 2 cặp cạnh đối song song
Ví dụ 1: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
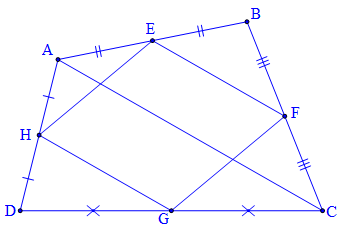
Ta có:
EF là đường trung bình của tam giác ABC, nên EF // AC (1)
Tương tự, HG là đường trung bình của tam giác ACD, nên HG // AC (2)
Từ (1) và (2) suy ra HG // EF
Tiếp theo:
FG là đường trung bình của tam giác CBD, nên FG // BD (3)
Tương tự, HE là đường trung bình của tam giác ABD, nên HE // BD (4)
Từ (3) và (4) suy ra HE // FG
Xét tứ giác EFGH có:
HG // EF và HE // FG;
Vậy Tứ giác EFGH là Hình bình hành do các cạnh đối song song. ( đpcm)
Ví dụ 2: Cho hình bình hành ABCD (AB > BC). Tia phân giác góc D cắt AB ở E, tia phân giác góc B cắt CD ở F. Chứng minh DEBF là hình bình hành.
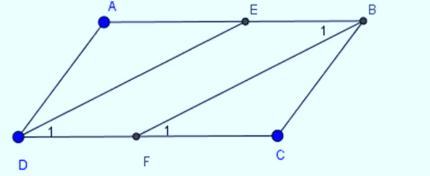
Ta có:
Góc B1 = D1 do đều bằng một ½ của hai góc bằng nhau B và D trong hình bình hành ABCD
AB // CD (ABCD là hình bình hành) => Góc B1 = F1 (so le trong)
Mà hai góc này lại ở vị trí đồng vị => DE // BF
Xét tứ giác DEBF có:
DE // BF (chứng minh trên)
BE // DF ( do AB // CD)
Vậy Tứ giác DEBF là Hình bình hành do các cạnh đối song song. ( đpcm)
Chứng minh tứ giác có 2 cặp cạnh đối bằng nhau
Ví dụ 3: Cho Tứ giác ABCD có ∆ABC = ∆CDA. Chứng minh rằng ABCD là Hình bình hành.
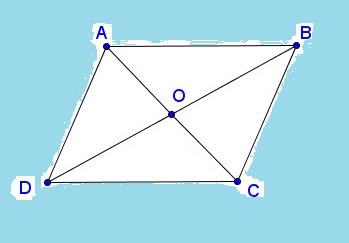
Theo bài ra, ta có:
∆ABC = ∆CDA => AD = BC và AB = CD
=> ABCD là hình bình hành dó có các cặp cạnh đối bằng nhau.
Chứng minh tứ giác có một cặp cạnh đối song song và bằng nhau
Ví dụ 4: Cho hình bình hành ABCD, gọi E là trung điểm AD, F là trung điểm BC. Chứng minh rằng BEDF là hình bình hành.
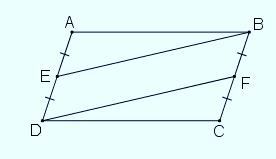
Ta có:
ABCD là hình bình hành => AD // BC và AD = BC
AD // BC => DE // BF (1)
E là trung điểm AD => DE = AD/2
F là trung điểm BC => BF = BC/2
Mà AD = BC (ABCD là hình bình hành)
DE = BF (2)
Từ (1) và (2) => Tứ giác DEBF là hình bình hành do có hai cạnh đối song song và bằng nhau.
Chứng minh tứ giác có các góc đối bằng nhau
Ví dụ 5: Cho Tứ giác ABCD có ∆ABC = ∆ ADC và ∆BAD = ∆BCD. Chứng minh rằng ABCD là hình bình hành.
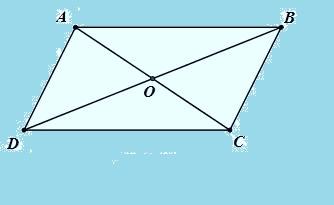
Theo bài ra, ta có:
∆ABC = ∆ADC => Góc ABC = Góc ADC (1)
∆BAD = ∆BCD => Góc BAD = Góc BCD (2)
Từ (1) và (2) suy ra Tứ giác ABCD là hình bình hành do các góc đối bằng nhau.
Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường
Ví dụ 6: Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Từ A kẻ AE vuông góc với BD, từ C kẻ CF vuông góc với BD. Chứng minh rằng Tứ giác AECF là hình bình hành.
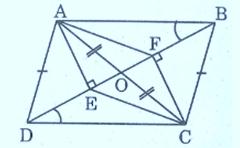
Ta có:
OA = OC (tính chất hình bình hành) (1)
Xét hai tam giác vuông AEO và CFO có:
Góc AEO = Góc CFO = 90°
OA = OC
Góc AOE = Góc COF (đối đỉnh)
Suy ra, ∆AEO = ∆CFO (cạnh huyền – góc nhọn) => OE = OF (2)
Từ (1) và (2) suy ra Tứ giác AECF là hình bình hành do có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Ví dụ 7: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng: AK // CI và DM = MN = NB
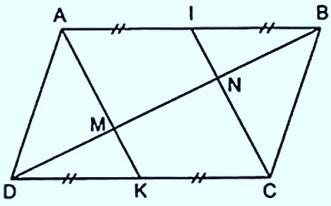
Ta có:
AB // CD và AB = CD ( do ABCD là hình bình hành)
I, K lần lượt là trung điểm AB, DC => AI=IB và DK = KC
Tứ giác AICK có cặp cạnh đối song song và bằng nhau (AI và KC) nên AICK là Hình bình hành nên AK // CI (điều phải chứng minh)
Tiếp theo ta có:
AM // IN và MK // NC
Xét tam giác AMB có:
AM // IN
AI = BI (I là trung điểm AB)
IN là đường trung bình của tam giác AMB
N là trung điểm MB => MN = NB (1)
Tương tự, xét tam giác DNC có:
MK // NC
DK = CK (K là trung điểm DC)
MK là đường trung bình của tam giác DNC
M là trung điểm DN => DM = NM (2)
Từ (1) và (2) suy ra DM = MN = NB (điều phải chứng minh).
Trên đây là hướng dẫn của Trung tâm Gia sư Tiến Bộ về cách chứng minh hình bình hành. Tùy từng bài toán mà chúng ta áp dụng cách nào cho hợp lý. Chúc cá
Hình học 8 - Tags: hình bình hành, toán 8