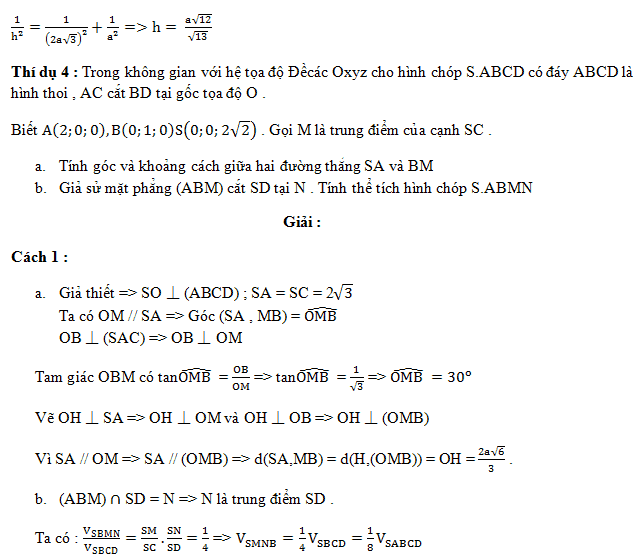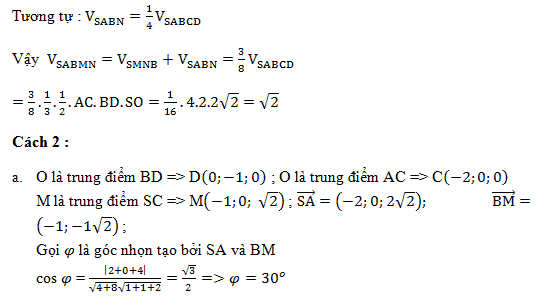Khoảng cách giữa 2 đường thẳng chéo nhau trong không gian lớp 11

Khái niệm hai đường thẳng chéo nhau trong không gian, cách tính khoảng cách giữa 2 đường thẳng chéo nhau lớp 11.

Thế nào là 2 đường thẳng chéo nhau? chứng minh 2 đường thẳng chéo nhau trong không gian như nào?

Định nghĩa hai đường thẳng chéo nhau?

Hai đường thẳng chéo nhau trong không gian là 2 đường thẳng không cùng nằm trong một mặt phẳng, không song song và không cắt nhau.

Cách chứng minh hai đường thẳng chéo nhau

Để chứng minh 2 đường thẳng d₁ và d₂ chéo nhau, ta sử dụng mệnh đề:

Nếu đường thẳng d₁ và d₂ chéo nhau thì tồn tại một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Hoặc dùng phương pháp phản chứng giả sử d₁ và d₂ không chéo nhau, tức là tồn tại một mặt phẳng (α) nào đó chứa cả hai đường thẳng d₁ và d₂. Từ đó lập luận để đưa đến điều mâu thuẫn.

Cách tính khoảng cách giữa 2 đường thẳng chéo nhau trong không gian:

Để xác định khoảng cách giữa hai đường thẳng chéo nhau: d₁ và d₂chúng ta có thể dùng một trong các cách dưới đây:

Dựa vào định nghĩa (Xác định đường vuông góc chung)

Cách này thường được tiến hành khi ta biết được hai đường thẳng d₁, d₂vuông góc với nhau . Khi đó ta làm như sau :

Bước 1: Xác định một mặt phẳng (P) chứa d₁ vuông góc với đường thẳng d₂

Tức là đường thẳng d₂ vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P) , trong đó có đường thẳng d₁.

Bước 2: Tìm giao điểm I của đường thẳng d₂ với mặt phẳng (P) . Từ I kẻ IH vuông góc với d₁, với H ∈ d₁. Khi đó IH là đoạn vuông góc chung của hai đường thẳng d₁, d₂.

Bước 3: Tính độ dài đoạn thẳng IH .

Ta thường vận dụng hệ thức lượng tam giác và tam giác đồng dạng ; định lý Pitago để tính độ dài đoạn IH.