A. Lý thuyết 1. Hai điểm đối xứng qua một điểm: Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm ấy.
A đối xứng với A’ qua O
⇔ O là trung điểm của AA’
Khi đó, ta còn nói: A’ đối xứng với A qua O hoặc A và A’ đối xứng với nhau qua O.
2. Quy ước: Điểm đối xứng với điểm O qua điểm O chính là điểm O.
3. Hai hình đối xứng qua một điểm: Hai hình gọi là đối xứng với nhau qua điểm O nếu một điểm bất kỳ thuộc hình này đối xứng với một điểm thuộc hình kia qua O và ngược lại.
4. Nhận xét: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì bằng nhau.
5. Hình có tâm đối xứng: Điểm O gọi là tâm đối xứng với hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
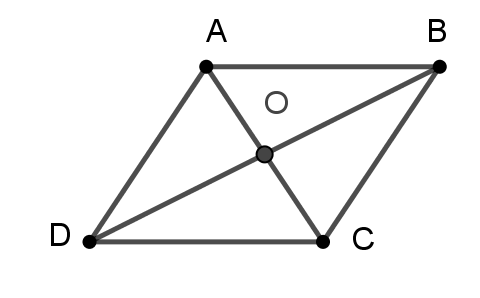
6. Định lý: Giao điểm của hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
O là tâm đối xứng của hình bình hành ABCD
B. Bài tập Bài toán 1: Cho
Bài toán 2: Cho tứ giác ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của câc cạnh AB, BC, CD, DA. Gọi E là điểm bất kỳ nằm ngoài tứ giác, F là điểm đối xứng với E qua M, G là điểm đối xứng với F qua Q, H là điểm đối xứng với G qua P. Chứng minh E là điểm đối xứng với H qua N.
Bài toán 3: Cho
a) A thuộc đường thẳng PQ
b) BCQP là hình bình hành
Bài toán 4: Cho hình bình hành ABCD. Trên cạnh AD lấy điểm E và trên cạnh BC lấy điểm F sao cho
Bài toán 5: Cho
Bài toán 6: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AD, BC ở E và F. Chứng minh E và F đối xứng nhau qua O.
Bài toán 7: Cho góc xOy. Điểm A nằm bên trong góc. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Tính số đo góc xOy để B đối xứng với C qua O.
Bài toán 8: Cho
Bài toán 9: Cho điểm O nằm trong tứ giác ABCD. Gọi E, F, G, H là điểm đối xứng của O theo thứ tự qua trung điểm của các cạnh AB, BC, CD, DA. Chứng minh EFGH là hình bình hành.
Bài toán 10: Cho tứ giác ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi E là điểm bất kỳ nằm ngoài tứ giác, F là điểm đối xứng với E qua M, G là điểm đối xứng với F qua N, H là điểm đối xứng với G qua P. Chứng minh E là điểm đối xứng với H qua Q.
Bài toán 11: Cho
a) Tứ giác MNIK là hình bình hành
b) Trọng tâm
Bài toán 12: Cho
Chứng minh rằng:
a) Ba đường thẳng AH, BI, CK đồng quy
b) Khi M di động trong tam giác thì đường thẳng OM luôn đi qua một điểm cố định.
Hình học 8 - Tags: đối xứng tâm , toán 8
