So sánh nghiệm của phương trình bậc 2 với một số
Phương pháp so sánh nghiệm của phương trình bậc 2 với số 0, với 1 số bất kỳ, phương trình quy về phương trình bậc 2.
Bài viết này Gia sư Tiến Bộ hướng dẫn các em cách so sánh nghiệm của PT bậc 2 với một số, đây là một dạng toán quen thuộc trong chương trình Toán lớp 9 với các bài toán có phương trình bậc hai.
Trước tiên các em cần phải ghi nhớ hệ thức Vi ét cho phương trình bậc 2 để áp dụng xác định dấu của các nghiệm.
Dấu của các nghiệm của phương trình bậc hai
Theo hệ thức Vi-ét nếu phương trình bậc hai : ![]() có nghiệm
có nghiệm ![]()
![]()
![]()
![]()
![]()
Do đó điều kiện để một phương trình bậc 2 :
– Có 2 nghiệm dương là: ![]()
– Có 2 nghiệm âm là: ![]()
– Có 2 nghiệm trái dấu là: ![]() (Khi đó hiển nhiên
(Khi đó hiển nhiên ![]() .
.
So sánh nghiệm của phương trình bậc 2 với số 0
Trong nhiều trường hợp ta cần so sánh nghiệm của phương trình bậc 2 với một số cho trước, trong đó có nhiều bài toán đòi hỏi tìm điều kiện để phương trình bậc 2: ![]()
![]()
![]()
Ví dụ 1: Tìm các giá trị của m để phương trình sau có ít nhất một nghiệm không âm:
![]() (1) .
(1) .
Cách 1: ![]() khi đó phương trình có 2 nghiệm
khi đó phương trình có 2 nghiệm ![]()
![]()
![]()
![]() .
.
Trước hết ta tìm điều kiện để phương trình (1) có 2 nghiệm đều âm. Điều kiện đó là: ![]()
Vậy điều kiện để phương trình (1) có ít nhất một nghiệm không âm là ![]()
Cách 2: ![]() ;
; ![]() .
.
-Nếu ![]()
![]() , thì phương trình (1) tồn tại nghiệm không âm.
, thì phương trình (1) tồn tại nghiệm không âm.
– Nếu ![]() thì phương trình có 2 nghiệm cùng dấu . Để thoả mãn đề bài ta phải có
thì phương trình có 2 nghiệm cùng dấu . Để thoả mãn đề bài ta phải có ![]() . Giải điều kiện P>0; S>0 được m>2 và m<0 không xảy ra.
. Giải điều kiện P>0; S>0 được m>2 và m<0 không xảy ra.
KL: ![]()
Cách 3: Giải phương trình (1) : ![]()
Ta có: ![]() .
.
Do ![]() nên ta phải có
nên ta phải có ![]() .
.
Ví dụ 2: Cho phương trình: ![]() (2) . Tìm giá trị của m để phương trình có hai nghiệm dương.
(2) . Tìm giá trị của m để phương trình có hai nghiệm dương.
Giải
Phương trình (2) có 2 nghiệm dương:
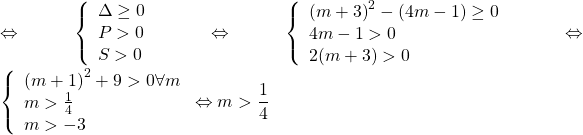
So sánh nghiệm của phương trình bậc 2 với một số bất kỳ
Trong nhiều trường hợp để so sánh nghiệm của phương trình bậc 2 với một số bất kỳ ta có thể quy về trường hợp so sánh nghiệm của phương trình bậc 2 với số 0:
Ví dụ 1: Tìm các giá trị của m để phương trình sau có ít nhất một nghiệm lớn hơn hoặc bằng 2:
![]() (1) .
(1) .
Cách 1: Đặt y=x-2![]() thay vào phương trình (1) ta được:
thay vào phương trình (1) ta được:
![]() (2).
(2).
Ta cần tìm m để phương trình (2) có ít nhất một nghiệm không âm.
![]() . Điều kiện để phương trình (2) có 2 nghiệm đều âm là:
. Điều kiện để phương trình (2) có 2 nghiệm đều âm là: 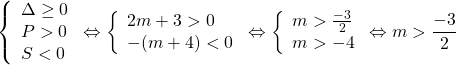 .
.
Vậy với ![]() thì phương trình (2) có ít nhất một nghiệm không âm tức là (1) có ít nhất một nghiệm lớn hơn hoặc bằng 2.
thì phương trình (2) có ít nhất một nghiệm không âm tức là (1) có ít nhất một nghiệm lớn hơn hoặc bằng 2.
Cách 2: Giải phương trình (1) ta được: ![]() .
.
Ta thấy ![]() nên chỉ cần tìm m để
nên chỉ cần tìm m để ![]() .
.
Ta có ![]()
– Nếu ![]() thì (3) có vế phải âm , vế trái dương nên (3) đúng.
thì (3) có vế phải âm , vế trái dương nên (3) đúng.
– Nếu ![]() thì (3)
thì (3) ![]()
Ta được ![]() .
.
Gộp ![]() và
và ![]() là giá trị cần tìm của m .
là giá trị cần tìm của m .
Ví dụ 2:Tìm các giá trị của m để phương trình sau có 2 nghiệm phân biệt nhỏ hơn 2:
![]() (1).
(1).
Giải:
Cách 1: Đặt ![]() thay vào (1) ta được :
thay vào (1) ta được :
![]()
![]() (2)
(2)
Cần tìm m để phương trình (2) có 2 nghiệm âm phân biệt. Ta giải điều kiện:
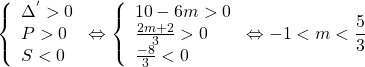
KL: Với ![]() thì phương trình (2) có nghiệm âm phân biệt, tức là phương trình (1) có 2 nghiệm phân biệt nhỏ hơn 2 .
thì phương trình (2) có nghiệm âm phân biệt, tức là phương trình (1) có 2 nghiệm phân biệt nhỏ hơn 2 .
Cách 2: Xét phương trình (1). Giải điều kiện:
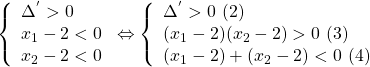
Giải (2) được: ![]() .
.
Giải (3): ![]()
Giải (4) : ![]() -4<0
-4<0![]() luôn đúng .
luôn đúng .
Vậy ta được -1<![]() .
.
Cách 3: Giải phương trình (1) : ![]() .
.
Nếu ![]() thì phương trình (1) có 2 nghiệm phân biệt:
thì phương trình (1) có 2 nghiệm phân biệt:
![]() ;
; ![]() . Do
. Do ![]() nên điều kiện để phương trình (1) có 2 nghiệm phân biệt nhỏ hơn 2 là:
nên điều kiện để phương trình (1) có 2 nghiệm phân biệt nhỏ hơn 2 là:
![]()
Vậy ta được -1<![]() .
.
Điều kiện về nghiệm của phương trình quy về phương trình bậc 2
Ví dụ 1: Tìm giá trị của m để phương trình sau có nghiệm.
![]() (1)
(1)
Giải:
Đặt ![]() .
.
Điều kiện để phương trình (1) có nghiệm là phương trình: ![]() có ít nhất một nghiệm không âm ,
có ít nhất một nghiệm không âm ,
Theo kết quả ở VD1 mục I , các giá trị của m cần tìm là: ![]()
Ví dụ 2: Tìm các giá trị của m để tập nghiệm của phương trình :
![]() (1) chỉ có 1 phần tử
(1) chỉ có 1 phần tử
Giải:
(1) ![]() (*)
(*) ![]()
Do đó tập nghiệm của phương trình (1) chỉ có một phần tử khi và chỉ khi có 1 và chỉ 1 nghiệm của phương trình (2) thoả mãn điều kiện ![]() . Đặt
. Đặt
x – m = y. Khi đó phương trình (2) trở thành 2![]() (3).
(3).
Cần tìm m để chỉ có một nghiệm của phương trình (3) thoả mãn ![]() .
.
Có 3 trường hợp xảy ra :
a) Phương trình (3) có nghiệm kép không âm:
![]()
b) Phương trình (3) có 2 nghiệm trái dấu:
![]()
c) Phương trình (3) có một nghiệm âm, nghiệm còn lại bằng 0:
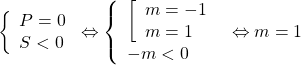 .
.
KL: ![]() hoặc -1
hoặc -1![]() .
.
Ví dụ 3: Tìm các giá trị của m để phương trình sau có 4 nghiệm phân biệt:
![]() (1)
(1)
Giải: (1)![]() . Đặt
. Đặt ![]()
khi đó (1) trở thành ![]() (2)
(2)
Với cách đặt ẩn phụ như trên , ứng với mỗi giá trị dương của y có hai giá trị của x .
Do đó: có 4 nghiệm phân biệt ![]() (2) có 2 nghiệm dương phân biệt.
(2) có 2 nghiệm dương phân biệt.
Do đó ở (2) ta phải có:
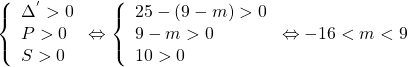
KL: ![]()
Bài tập tự giải
Bài 1: Tìm các giá trị của m để tồn tại nghiệm không âm của phương trình: ![]()
Bài 2: Tìm các giá trị của m để phương trình sau có nghiệm:
![]()
Bài 3: Tìm các giá trị của m để phương trình:
![]() có 2 nghiệm phân biệt lớn hơn -1.
có 2 nghiệm phân biệt lớn hơn -1.
Bài 4: Tìm các giá trị của m để phương trình: ![]() có ít nhất 1 nghiệm lớn hơn hoặc bằng -2.
có ít nhất 1 nghiệm lớn hơn hoặc bằng -2.
Bài 5: Tìm các giá trị của m để tập nghiệm của phương trình:
![]()
a) Có 4 phần tử.
b) Có 3 phần tử.
c) Có 2 phần tử.
d) Có 1 phần tử.
Đại số 9 - Tags: nghiệm, phương trình, phương trình bậc 2, so sánh nghiệm