Ứng dụng vectơ chứng minh bất đẳng thức
Phương pháp dùng vectơ (tích vô hướng của 2 vecto) để chứng minh bất đẳng thức là một phương pháp mới để chứng minh BĐT của Toán THPT.
Cụ thể của phương pháp chứng minh bất đẳng thức bằng vectơ ta dùng bất đẳng thức sau:
Chứng minh BĐT vectơ trên:
Ta có:
Tích vô hướng của 2 vectơ ![]()
![]()
![]()
![]()
Do ![]() , nên:
, nên: ![]()
![]()
![]()
BÀI TẬP CÓ LỜI GIẢI
Bài toán 1: Cho ![]() ABC, CMR: cosA + cosB + cosC
ABC, CMR: cosA + cosB + cosC ![]() .
.
Giải
Thiết lập các vectơ đơn vị ![]() ,
, ![]() ,
, ![]() trên các cạnh AB, BC, AC của
trên các cạnh AB, BC, AC của ![]() ABC, ta được:
ABC, ta được:
![]()
![]()
![]()
Mặt khác ta luôn có:
![]()
![]()
![]() , đpcm.
, đpcm.
Bài toán 2: Cho ![]() ABC, CMR:
ABC, CMR: ![]() .
.
Giải
Gọi O là tâm đường tròn ngoại tiếp ![]() ABC, ta nhận được:
ABC, ta nhận được:
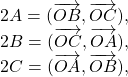
Mặt khác:
![]()
![]()
![Rendered by QuickLaTeX.com \Leftrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="http://abcdonline.vn/wp-content/ql-cache/quicklatex.com-21bce0183a60d3d9f16cd8cfa8d4ceba_l3.png" height="466" width="629" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[c\text{os}2A+c\text{os}2B+c\text{os}2C\ge -\frac{3}{2}$, đpcm <strong>Bài toán 3: </strong>Chứng minh $ \displaystyle \forall x,y\in $<strong>R</strong>, ta có<strong>: </strong>$ \displaystyle \left| \frac{(x+y)(1-xy)}{(1+{{x}^{2}})(1+{{y}^{2)}}} \right|\le \frac{1}{2}$ (*) <em>Giải</em> Ta có (*) $ \displaystyle \Leftrightarrow \left| \frac{x(1-{{y}^{2}})+y(1-{{x}^{2}})}{(1+{{x}^{2}})(1+{{y}^{2}})} \right|\le \frac{1}{2}$ $ \displaystyle \Leftrightarrow \left| \left( \frac{2x}{1+{{x}^{2}}} \right).\left( \frac{1-{{y}^{2}}}{1+{{y}^{2}}} \right)+\left( \frac{2y}{1+{{y}^{2}}} \right).\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right) \right|\le 1$ Đặt: $ \displaystyle \begin{array}{l}\vec{a}=\left( \frac{2x}{1+{{x}^{2}}},\frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right)\\\vec{b}=\left( \frac{1-{{y}^{2}}}{1+{{y}^{2}}},\frac{2y}{1+{{y}^{2}}} \right)\end{array}$ Suy ra : $ \displaystyle \left| {\vec{a}} \right|=\left| {\vec{b}} \right|=1$ Mà $ \displaystyle \left| \vec{a}.\vec{b} \right|\le \left| {\vec{a}} \right|.\left| {\vec{b}} \right|$. Vậy $ \displaystyle \left| \vec{a},\vec{b} \right|\le 1$ (đpcm). <strong>Bài toán 4:</strong> Cho ba số $ \displaystyle x,$ $ \displaystyle y,$ $ \displaystyle z$ thỏa hệ thức $ \displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=xy+yz+xz.$ Chứng minh rằng $ \displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-(xy+yz+zx)\ge 0.$ <em>Giải</em> Trong không gian với hệ tọa độ Đề-các vuông góc Oxy cho các vectơ : $ \displaystyle \vec{u}=(x,y,z),$ $ \displaystyle \vec{v}=(y,z,x)$ Vì $ \displaystyle \vec{u}.\vec{v}=\left| {\vec{u}} \right|.\left| {\vec{v}} \right|\cos (\vec{u},\vec{v})$ $ \displaystyle \Leftrightarrow $ $ \displaystyle xy+yz+xz=({{x}^{2}}+{{y}^{2}}+{{z}^{2}})\cos (\vec{u},\vec{v}).$ Mặt khác ta có $ \displaystyle xy+yz+zx={{x}^{2}}+{{y}^{2}}+{{z}^{2}}$ nếu $ \displaystyle \cos (\vec{u},\vec{v})=1$ nghĩa là $ \displaystyle \vec{u}$ và $ \displaystyle \vec{v}$ cùng hướng. Vì $ \displaystyle \left| {\vec{u}} \right|=\left| {\vec{v}} \right|$ do đó $ \displaystyle \vec{u}=\vec{v}$ nghĩa là $ \displaystyle x=y=z$. Do đó ta có: $ \displaystyle 0\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-(xy+yz+zx).$ <strong>Bài toán 5</strong>: Cho bốn số thực tùy ý $ {{a}_{1}},{{a}_{2}},{{b}_{1}},{{b}_{2}}$. Chứng minh: $ \sqrt{{{a}_{1}}^{2}+{{a}_{2}}^{2}}+\sqrt{{{b}_{1}}^{2}+{{b}_{2}}^{2}}\ge \sqrt{{{({{a}_{1}}+{{b}_{1}})}^{2}}+{{({{a}_{2}}+{{b}_{2}})}^{2}}}$ Giải Xét các vectơ:$ \overrightarrow{u}=({{a}_{1}},{{a}_{2}});\overrightarrow{v}=({{b}_{1}},{{b}_{2}})\Rightarrow \overrightarrow{u}+\overrightarrow{v}=({{a}_{1}}+{{b}_{1}},{{a}_{2}}+{{b}_{2}})$ Áp dụng :$ \left| \overrightarrow{u} \right|+\left| \overrightarrow{v} \right|\ge \left| \overrightarrow{u}+\overrightarrow{v} \right|$ $ \Rightarrow\]" title="Rendered by QuickLaTeX.com"/> \sqrt{{{a}_{1}}^{2}+{{a}_{2}}^{2}}+\sqrt{{{b}_{1}}^{2}+{{b}_{2}}^{2}}\ge \sqrt{{{({{a}_{1}}+{{b}_{1}})}^{2}}+{{({{a}_{2}}+{{b}_{2}})}^{2}}}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-e7b18f5bb88eed49050b5f9e13bb6c7e_l3.png)
Đẳng thức xảy ra khi ![]() cùng hướng
cùng hướng![]()
Bài toán 6: Cho 6 số thực a, b, c, d, x, y, z thỏa mãn: a + b + c = 2; ax + by + cz = 6
Chứng minh rằng:![]()
HD: Đặt ![]()
BÀI TẬP TỰ GIẢI
1. Cho ![]() ABC, CMR:
ABC, CMR: ![]() .
.
2. CMR:
a) ![]() .
.
b) ![]()
3. Tìm giá trị lớn nhất của biểu thức:![]()
4. Cho x, y, z là ba số dương và x + y + z ![]() 1
1
Chứng minh rằng:![]()
5. (Đại học khối B 2006).Cho x,y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức
![]()
6. Cho ba số thực x, y, z tùy ý.Chứng minh:
![]()
