Ứng dụng vectơ giải các bài toán quỹ tích điểm

Phương pháp chung bài toán quỹ tích bằng vectơ

Với các bài toán quỹ tích ta cần nhớ :

Nếu \displaystyle \left| {\overrightarrow{{MA}}} \right|=\left| {\overrightarrow{{MB}}} \right|

, với A, B cho trước thì M thuộc đường trung trực của đoạn AB.

\displaystyle \left| {\overrightarrow{{MC}}} \right|=k\left| {\overrightarrow{{AB}}} \right|

, với A, B, C cho trước thì M thuộc đường tròn tâm C, bán kính bằng k.AB.

Nếu \displaystyle \overrightarrow{{MA}}=k\overrightarrow{{BC}}

, với A, B, C cho trước thì:

– Với \displaystyle k\in R điểm M thuộc đường thẳng qua A song song với BC.

– Với \displaystyle k\in {{R}^{+}} điểm M thuộc nửa đường thẳng qua A song song với BC theo hướng \overrightarrow{BC}.

– Với \displaystyle k\in R điểm M thuộc nửa đường thẳng qua A song song với BC ngược hướng \overrightarrow{BC}.

Các bài toán quỹ tích có lời giải

Bài toán 1: Cho \DeltaABC, tìm tập hợp những điểm M thỏa mãn

a. \displaystyle \overrightarrow{{MA}}+k\overrightarrow{{MB}}-k\overrightarrow{{MC}}=\vec{0}. (1)

b. \displaystyle (1-k)\overrightarrow{{MA}}+\overrightarrow{{MB}}-k\overrightarrow{{MC}}=\vec{0}. (2)

Giải

a. Ta biến đổi (1) về dạng:

\displaystyle \overrightarrow{{MA}}=k(\overrightarrow{{MC}}-\overrightarrow{{MB}})\Leftrightarrow \overrightarrow{{MA}}=k\overrightarrow{{BC}}

⇔ \displaystyle M thuộc đường thẳng qua A song song với BC.

b. Ta biến đổi (2) về dạng:

\displaystyle \overrightarrow{{MA}}+\overrightarrow{{MB}}-k(\overrightarrow{{MA}}+\overrightarrow{{MC}})=\vec{0}.                                      (3)

Gọi E, F theo thứ tự là trung điểm của AB và AC, ta được:

(3) ⇔ \displaystyle 2\overrightarrow{{ME}}-2k\overrightarrow{{MF}}=\vec{0}\Leftrightarrow \overrightarrow{{ME}}=k\overrightarrow{{MF}}

⇔ \displaystyle M thuộc đường trung bình EF của \DeltaABC.

Bài toán 2: Trên tia Ox và Oy của \widehat{xOy} lấy hai điểm M, N sao cho OM + ON = a (a là độ dài cho trước). Tìm quỹ tích trung điểm I của đoạn MN.

Giải

Lấy hai điểm {{M}_{0}}, {{N}_{0}} thuôạ Ox, Oy sao cho:

O{{M}_{0}}=O{{N}_{0}}=\frac{a}{2}.

Giả sử OM=k thì ON=a-k, với 0\le k\le a, khi đó:

\overrightarrow{OM}=\frac{2k}{a}\overrightarrow{O{{M}_{0}}}  và \overrightarrow{ON}=\frac{2(a-k)}{a}\overrightarrow{O{{N}_{0}}}.

Vì I là trung điểm của đoạn MN, ta được:

\overrightarrow{OI}=\frac{1}{2}(\overrightarrow{OM}+\overrightarrow{ON})=\frac{1}{2}\text{ }\!\![\!\!\text{ }\frac{2k}{a}\overrightarrow{O{{M}_{0}}}+\frac{2(a-k)}{a}\overrightarrow{O{{N}_{0}}}]

\Leftrightarrow \overrightarrow{O{{M}_{0}}}+\overrightarrow{{{M}_{0}}I}=\frac{k}{a}\overrightarrow{O{{M}_{0}}}+\frac{2(a-k)}{a}\overrightarrow{O{{N}_{0}}}

\displaystyle \Leftrightarrow \overrightarrow{{{M}_{0}}I}=(\frac{k}{a}-1)\overrightarrow{O{{M}_{0}}}+\frac{a-k}{a}\overrightarrow{O{{N}_{0}}}

\begin{array}{l}\Leftrightarrow a\overrightarrow{{{M}_{0}}I}=(a-k)(\overrightarrow{O{{N}_{0}}}-\overrightarrow{O{{M}_{0}}})\\\Leftrightarrow \overrightarrow{{{M}_{0}}I}=\frac{a-k}{A}\overrightarrow{{{M}_{0}}{{N}_{0}}}\end{array}

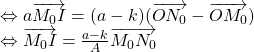
Vậy quỹ tích I thuộc đoạn {{M}_{0}}{{N}_{0}}.     

Bài toán 3: Cho tam giác ABC và trung tuyến AM. Một đường thẳng song song với AB cắt các đoạn thẳng AM, AC và BC lần lượt tại D, E và F. Một điểm G nằm trên cạnh AB sao cho FG song song AC. Chứng minh rằng hai tam giác ADE và BFG có diện tích bằng nhau.

Giải

Ta đặt: \displaystyle \overrightarrow{{CA}}=\vec{a};\overrightarrow{{CB}}=\vec{b} .

Khi đó \displaystyle \overrightarrow{{CM}}=\frac{{\vec{b}}}{2}\overrightarrow{{CE}}=k\overrightarrow{{CA}}=k\vec{a}

Vì E nằm ngoài đoạn thẳng AC nên có số k sao cho \displaystyle \overrightarrow{{CE}}=k\overrightarrow{{CA}}=k\vec{a}, với 0< k< 1.

Khi đó \displaystyle \overrightarrow{{CF}}=k\overrightarrow{{CB}}=k\vec{b}

Điểm D nằm trên AM và EF nên có hai số x và y sao cho:

\displaystyle \overrightarrow{{CD}}=x\overrightarrow{{CA}}+(1-x)\overrightarrow{{CM}}=y\overrightarrow{{CE}}+(1-y)\overrightarrow{{CF}}

Hay \displaystyle x\vec{a}+\frac{{1-x}}{2}\vec{b}=ky\vec{a}+k(1-y)\vec{b}

Vì hai vectơ \displaystyle \vec{a},\vec{b} không cùng phương nên x = ky và \displaystyle \frac{{1-x}}{2}=k(1-y).

Suy ra x = 2k -1,do đó \displaystyle \overrightarrow{{CD}}=(2k-1)\vec{a}+(1-k)\vec{b}

Ta có:

\displaystyle \overrightarrow{{ED}}=\overrightarrow{{CD}}-\overrightarrow{{CE}}=(2k-1)\vec{a}+(1-k)\vec{b}-k\vec{a}=(1-k)(\vec{b}-\vec{a})=(1-k)\overrightarrow{{AB}}

Chú ý rằng vì \displaystyle \overrightarrow{{CF}}=k\overrightarrow{{CB}} hay \displaystyle \overrightarrow{{AB}}+\overrightarrow{{BG}}=k\overrightarrow{{AB}}

Suy ra (1-k)\overrightarrow{AB}=\overrightarrow{GB}

Do đó ED = GB. Như vậy, hai tam giác ADE và BFG có các cạnh đáy ED và GB bằng nhau (bằng khoảng cách giữa hai đường thẳng song song) nên có diện tích bằng nhau.

Bài toán 4: Cho hình vuông ABCD, điểm M nằm trên đoạn thẳng AC sao cho AM=\frac{AC}{4}. Gọi N là trung điểm CD.Chứng minh rằng BMN là tam giác vuông cân.

Giải

Đặt \displaystyle \overrightarrow{{AD}}=\vec{a},\overrightarrow{{AB}}=\vec{b}

Khi đó:

\displaystyle {\overrightarrow{{AM}}=\frac{1}{4}\overrightarrow{{AC}}=\frac{1}{4}(\vec{a}+\vec{b})}

\displaystyle {\overrightarrow{{AN}}=\overrightarrow{{AD}}+\overrightarrow{{DN}}=\vec{a}+\frac{{\vec{b}}}{2}}

Ta có: \displaystyle \overrightarrow{{MB}}.\overrightarrow{{MN}}=\frac{1}{{16}}(-\vec{a}+3\vec{b})(3\vec{a}+\vec{b})

\displaystyle =\frac{1}{{16}}(-3{{\vec{a}}^{2}}+3{{\vec{b}}^{2}}+8\vec{a}.\vec{b})=0

\displaystyle {{\overrightarrow{{MB}}}^{2}}=\frac{1}{{16}}{{(-\vec{a}+3\vec{b})}^{2}}=\frac{1}{{16}}({{\vec{a}}^{2}}+9{{\vec{b}}^{2}}-6\vec{a}.\vec{b})=\frac{5}{8}{{\vec{a}}^{2}}

\displaystyle {{\overrightarrow{{MN}}}^{2}}=\frac{1}{{16}}{{(3\vec{a}+\vec{b})}^{2}}=\frac{1}{{16}}(9{{\vec{a}}^{2}}+{{\vec{b}}^{2}}+6\vec{a}.\vec{b})=\frac{5}{8}{{\vec{a}}^{2}}

Vậy MB vuông góc với MN và MB =MN, tam giác BMN vuông cân tại đỉnh M

Bài toán 5: Chứng minh rằng trong hình bình hành ta có: tổng các bình phương của hai đường chéo bằng tổng các bình phương của các cạnh

Giải

Cho hình bình hành ABCD,ta phải chứng minh:

\displaystyle \begin{array}{*{20}{l}} {A{{C}^{2}}+B{{D}^{2}}=2(A{{B}^{2}}+A{{D}^{2}})} \end{array}

Ta có:

\displaystyle {A{{C}^{2}}+B{{D}^{2}}={{{\overrightarrow{{AC}}}}^{2}}+{{{\overrightarrow{{BD}}}}^{2}}}

\displaystyle {={{{(\overrightarrow{{AB}}+\overrightarrow{{AD}})}}^{2}}+{{{(\overrightarrow{{BC}}+\overrightarrow{{BA}})}}^{2}}}

\displaystyle {=2(A{{B}^{2}}+A{{D}^{2}})+2(\overrightarrow{{AB}}.\overrightarrow{{AD}}+\overrightarrow{{BA}}.\overrightarrow{{BC}})}

Do \displaystyle \overrightarrow{{AB}}.\overrightarrow{{AD}}+\overrightarrow{{BA}}.\overrightarrow{{BC}}=0, \displaystyle \overrightarrow{{BA}}=-\overrightarrow{{AB}}, \displaystyle \overrightarrow{{BC}}=\overrightarrow{{AD}}

nên: \displaystyle \overrightarrow{{AB}}.\overrightarrow{{AD}}+\overrightarrow{{BA}}.\overrightarrow{{BC}}=0

Vậy ta có: \displaystyle A{{C}^{2}}+B{{D}^{2}}=2(A{{B}^{2}}+A{{D}^{2}})

Bài tập

Bài 1: Cho\Delta ABCvuông cân tại C. Trên các cạnhBC,CA,ABlần lượt lấy các điểm M,N,P sao cho: \frac{MB}{MC}=\frac{NC}{NA}=\frac{PA}{PB}

Chứng minh rằng:

a. CP\bot MN

b. CP=MN.

Bài 2: Cho \Delta ABC có đường cao CH. Gọi I, K lần lượt là trung điểm của các cạnh AB và CH. Một đường thẳng d di động luôn luôn song song với cạnh AB cắt cạnh AC ở M và cắt cạnh BC ở N. Dựng hình chữ nhật MNPQ với hai điểm P, Q nằm trên cạnh AB. Gọi J là tâm hình chữ nhật MNPQ. Chứng tỏ rằng ba điểm I, K, J thẳng hàng.

Bài 3: Cho hai hình vuông ABCD và BKMN có chung đỉnh B và đỉnh M nằm trên DB kéo dài. Chứng minh rằng trung tuyến BE của \Delta ABK nằm trên đường thẳng chứa đường cao BH của \Delta BNC.

Bài 4: Qua trọng tâm G của \Delta ABC vẽ đường thẳng \Delta cắt các cạnh AB và AC tại M và N. Chứng minh: \frac{MB}{MA}+\frac{NC}{NA}=1.

Bài 5: Cho \Delta ABC. Từ một P điểm P thay đổi nằm trong mặt phẳng của tam giác ta kẻ các đường thẳng song song với CA, CB lần lượt cắt CA, CB tại Q và R. Đường thẳng d nối Q với trung điểm I của CA cắt đường thẳng {{d}^{'}} nối R với trung điểm J của CB tại S. Chứng minh rằng đường thẳng PS luôn đi qua một điểm cố định.

Bài 6: Cho tam giac ABC có trọn tâm G và nội tiếp đường tròn tâm O bán kính R. Chứng minh rằng: O{{G}^{2}}={{R}^{2}}-\frac{1}{9}({{a}^{2}}+{{b}^{2}}+{{C}^{2}})

Hình học 10 - Tags: ,