Vị trí tương đối của đường thẳng và đường tròn

A. Lý thuyết

1. 

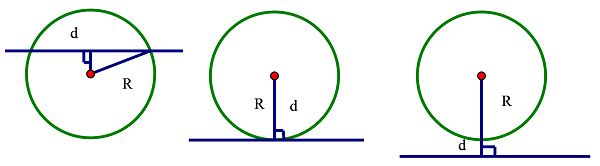
Vị trí tương đối của đường thẳng và đường trònSố điểm chungHệ thức giữa d và R
Đường thẳng và đường tròn cắt nhau2d<R
Đường thẳng và đường tròn tiếp xúc nhau1d=R
Đường thẳng và đường tròn không giao nhau0d>R

Vị trí tương đối của đường thẳng và đường tròn

2. Định lý

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

B. Bài tập

Bài 1: Cho tam giác ABC có AB=8, AC=6, BC=10. Vẽ đường tròn (C; CA)

a. Chứng minh AB là tiếp tuyến của đường tròn (C)

b. Xác định vị trí tương đối của đường thằng BC với đường tròn (C)

Bài 2: Cho điểm M nằm trên đường tròn (O; R). A là điểm nằm trên đường thẳng vuông góc với OM tại M. Vẽ dây MN vuông góc với OA tại H. Chứng minh rằng:

a. AM là tiếp tuyến của đường tròn (O)

b. AN là tiếp tuyến của đường tròn (O)

Bài 3: Cho đường tròn (O;R),đường kính AB. M là điểm thuộc đường tròn (O); (M khác A, B). BM cắt tiếp tuyến tại A của đường tròn (O) ở C.

a. Chứng minh rằng: MB.BC=4{{R}^{2}}

b. Đường thẳng qua O song song với BC cắt AC tại D. Chứng minh DM là tiếp tuyến của đường tròn (O)

Bài 4: Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.

a. Chứng minh rằng bốn điểm A, D, H, E cùng nằm trên một đường tròn(Gọi tâm của nó là O)

b. Gọi M là trung điểm của BC. Chứng minh rằng ME là tiếp tuyến của đường tròn tâm (O)

Bài 5: Cho đường tròn (O; R) đường kính AB. Vẽ dây cung AC sao cho \widehat{{CAB}}={{30}^{o}}

. Trên tia đối của tia BA lấy điểm M sao cho BM=R. Chứng minh rằng:

a. MC là tiếp tuyến của đường tròn (O)

b. M{{C}^{2}}=3{{R}^{2}}

Bài 6: Cho tam giác ABC vuông ở A có AB=8cm, AC=15cm. Vẽ đường cao AH. Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD, cắt AC ở E.

a. Chứng minh rằng HE là tiếp tuyến của đường tròn

b. Tính độ dài HE

Bài 7: Từ một điểm M nằm ngoài đường tròn(O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên tia OB lấy điểm C sao cho BC=BO. Chứng minh rằng \widehat{{BMC}}=\frac{1}{2}\widehat{{BMA}}

Bài 8: Cho đường tròn \left( {O;~R} \right) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. Chứng minh rằng \widehat{{BAC}}={{60}^{o}} khi và chỉ khi OA=2R

Bài 9: Từ một điểm A ở ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt AC tại N.Đường thằng vuông góc với OV tại O cắt AB tại M.

a. Chứng minh tứ giác AMON là hình thoi

b. Điểm A phải cách O một khoảng bao nhiêu để MN mà tiếp tuyến của (O)

Bài 10: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Các tiếp tuyến của đường tròn vẽ từ A và C cắt nhau tại M. Trên tia AM lấy điểm D sao cho AD=BC. Chứng minh rằng:

a. Tứ giác ABCD là hình bình hành

b. Ba đường thằng AC, BD, OM đồng quy

Bài 11: Cho đường tròn (O), dây cung CD. Qua O vẽ OH\bot CD tại H, cắt tiếp tuyến tại C của đường tròn (O) tại M. Chứng minh MD là tiếp tuyến của (O).

Bài 12: Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tia Ax\bot AB và By\bot AB ở cùng phía nửa đường tròn. Gọi I là một điểm trên nửa đường tròn. Tiếp tuyến tại I cắt Ax tại C và By tại D. Chứng minh AC+BD=CD

Bài 13: Cho đường tròn (O;5cm). Từ điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho MA\bot MB tại M.

a. Tính MA và MB

b. Qua trung điểm I của cung nhỏ AB, vẽ một tiếp tuyến OA, OB tại C và D. Tính CD

Bài 14: Cho đường tròn (O), Từ điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho \widehat{{AMB}}={{60}^{o}}.Biết chu vi tam giác MAB là 18cm. Tính độ dài dây AB

Hình học 9 - Tags: ,