10 bài tập Hình học nâng cao lớp 7 có đáp án

Đây là bài thứ 2 of 4 trong chuyên đề Toán nâng cao lớp 7

Nâng Cao Và Phát Triển Toán 7- Vũ Hữu Bình tập 1, 2
10 bài tập Hình học nâng cao lớp 7 có đáp án
Bài tập nâng cao và một số chuyên đề Toán 7 – Bùi Văn Tuyên
Sách bồi dưỡng Toán 7 tập một – Vũ Hữu Bình

Tăng cường khả năng giải Toán Hình học cho học sinh lớp 7 với 10 bài tập hình học nâng cao có lời giải được Gia sư Tiến Bộ chia sẻ dưới đây.

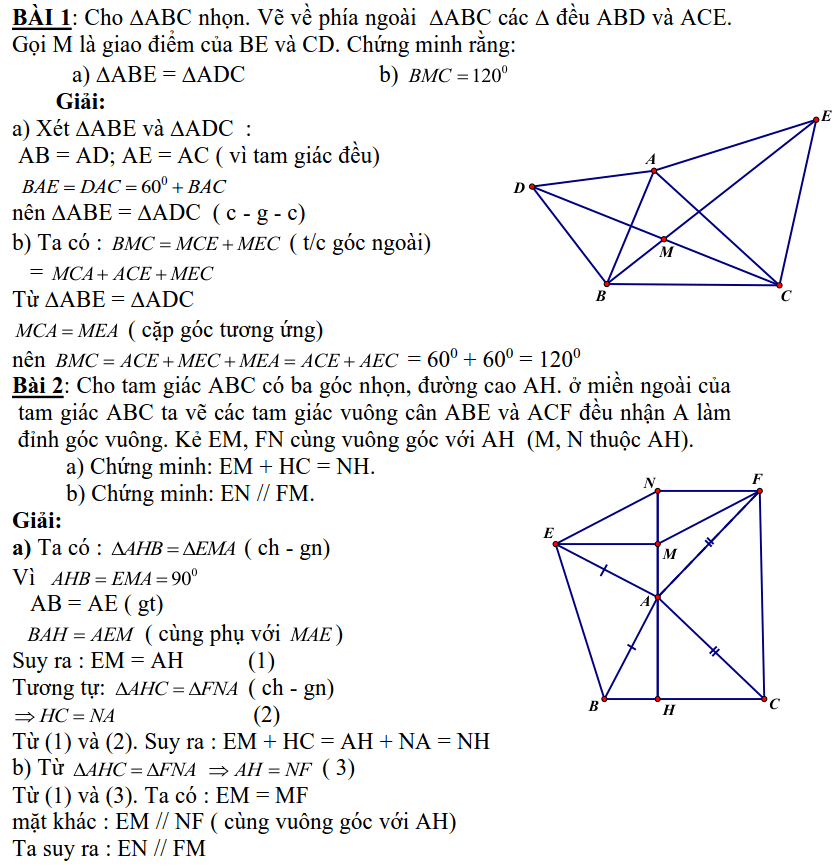
BÀI 1: Cho ∆ABC nhọn. Vẽ về phía ngoài ∆ABC các ∆ đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:

a) ∆ABE = ∆ADC

b) $\widehat{{BMC}}={{120}^{0}}$

Bài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).

a) Chứng minh: EM + HC = NH.

b) Chứng minh: EN // FM.

Bài 3:Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi DAPQ bằng 2.

Chứng minh rằng : $\displaystyle \widehat{{PCQ}}={{45}^{0}}$

Bài 4:Cho tam giác vuông cân ABC (AB = AC), tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D.

a) Chứng minh rằng: BE = CD; AD = AE.

b) Gọi I là giao điểm của BE và CD. AI cắt BC ở M, chứng minh rằng các DMAB; MAC là tam giác vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC.

Bài 5: Cho tam giác cân ABC (AB = AC ). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:

a) DM = EN

b) Đường thẳng BC cắt MN tại trung điểm I của MN.

c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
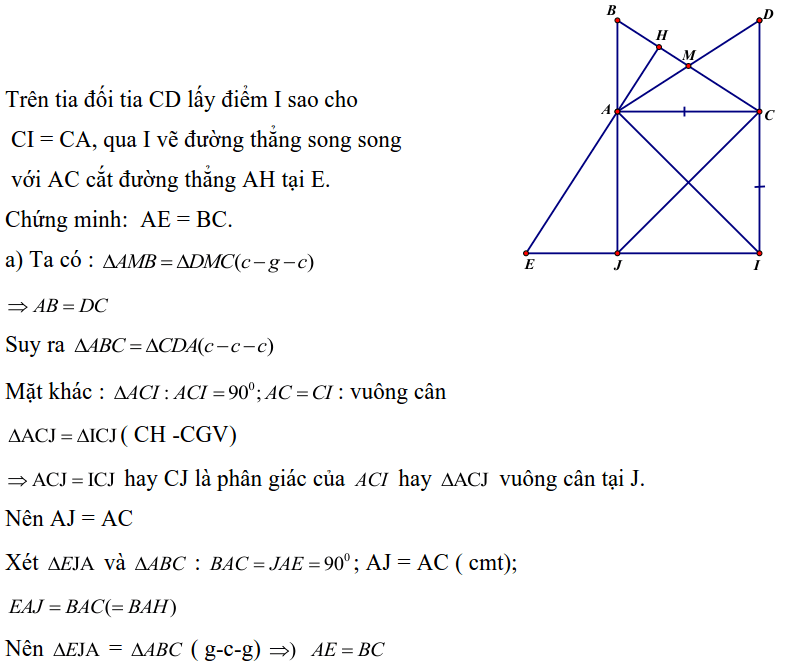
Bài 6: Cho tam giác vuông ABC: $\displaystyle \widehat{A}={{90}^{0}}$

, đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE = BC.

Bài 7: Cho ba điểm B, H, C thẳng hàng, BC = 13 cm, BH = 4 cm, HC = 9 cm. Từ H vẽ tia Hx vuông góc với đường thẳng BC. Lấy A thuộc tia Hx sao cho HA = 6 cm.

a) ∆ABC là ∆ gì ? Chứng minh điều đó.

b) Trên tia HC lấy điểm D sao cho HD = HA. Từ D vẽ đường thẳng song song với AH cắt AC tại Chứng minh: AE = AB

Bài 8: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:

a) AC = EB và $\displaystyle$ AC // BE

b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng minh ba điểm I , M , K thẳng hàng

c) Từ E kẻ $EH\bot BC$ $\left( {H\in BC} \right)$ . Biết $\widehat{{HBE}}$ = 50^o ; $\widehat{{MEB}}$ =25^o . Tính $\widehat{{HEM}}$ và $\widehat{{BME}}$
Bài 9: Cho tam giác ABC cân tại A có $\widehat{A}={{20}^{0}}$ , vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân giác của góc ABD cắt AC tại M. Chứng minh:

a) Tia AD là phân giác của góc BAC b) AM = BC
Bài 10: Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh AK + CE = BE.