Đề thi giao lưu Olympic môn Toán 7 huyện Kinh Môn 2018-2019
- Đề thi HSG Toán 7 thị xã Hương Trà 2020-2021
- Đề thi HSG Toán 7 THCS Cẩm Bình, huyện Cẩm Xuyên 2020-2021
- Đề thi HSG Toán 7 thành phố Sầm Sơn 2020-2021
- Đề thi HSG Toán 7 huyện Lập Thạch, Vĩnh Phúc 2020-2021
- Đề thi HSG Toán 7 huyện Lạng Giang 2020-2021
- Đề thi HSG Toán 7 huyện Phú Xuyên 2020-2021
- Đề thi HSG Toán 7 cấp trường huyện Nam Trực 2020-2021
- Đề thi HSG Toán 7 huyện Ngọc Lặc, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 quận Ô Môn, Cần Thơ 2020-2021
- Đề thi HSG Toán 7 thành phố Quảng Ngãi 2020-2021
- Đề thi HSG Toán 7 huyện Như Thanh, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 huyện Nho Quan, Ninh Bình 2020-2021
- Đề thi HSG Toán 7 thành phố Ninh Bình 2020-2021
- Đề thi HSG Toán 7 thành phố Bắc Ninh 2020-2021
- Đề thi HSG Toán 7 huyện Tiên Du, Bắc Ninh 2020-2021
- Đề thi HSG Toán 7 huyện Bố Trạch 2020 – 2021
- Đề thi HSG Toán 7 huyện Hà Trung 2020-2021
- Đề thi HSG Toán 7 THCS Kim Đồng, Hội An 2020 – 2021
- Đề thi HSG Toán 7 huyện Tam Đảo 2020 – 2021
- Đề thi HSG Toán 7 huyện Thọ Xuân, Thanh Hóa 2020-2021
- Đề thi Olympic Toán 7 huyện Quốc Oai 2020-2021
- Đề thi HSG Toán 7 huyện Nam Đàn 2020 – 2021
- Đề thi Olympic Toán 7 TP Hồ Chí Minh tháng 4 năm 2021
- Đề thi HSG Toán 7 thị xã Nghi Sơn 2020-2021
- Đề thi HSG Toán 7 huyện Thiệu Hóa, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 thành phố Vinh 2020-2021
- Đề thi HSG Toán 7 thị xã Thái Hòa, Nghệ An 2020-2021
- Đề thi HSG Toán 7 huyện Lương Tài, Bắc Ninh 2020-2021
- Đề thi HSG Toán 7 huyện Trực Ninh, Nam Định 2020-2021
- Đề thi HSG Toán 7 huyện Lục Nam 2020-2021
- Đề thi HSG Toán 7 huyện Nga Sơn, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 huyện Bá Thước, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 huyện Cao Lộc 2020-2021
- Đề giao lưu thành viên các CLB môn Toán lớp 7 huyện Quảng Xương 2020-2021
- Đề thi HSG Toán 7 huyện Yên Lạc, Vĩnh Phúc 2020-2021
- Đề thi HSG Toán 7 huyện Thạch Thành 2020-2021
- Đề thi HSG Toán 7 huyện Hoằng Hóa, Thanh Hóa 2020-2021 có đáp án
- Đề thi Olympic Toán 7 huyện Nghĩa Đàn, Nghệ An 2020-2021
- Đề thi HSG Toán 7 huyện Nghi Lộc, Nghệ An 2020-2021
- Đề thi chọn lớp CLC môn Toán 7 thị xã Cửa Lò 2020-2021
- Đề thi HSG Toán 7 huyện Đô Lương, Nghệ An 2020-2021
- Đề thi HSG Toán 7 huyện Kỳ Anh, Hà Tĩnh 2020-2021
- Đề thi HSG Toán 7 huyện Yên Định, Thanh Hóa 2020-2021
- Đề thi HSG Toán 7 huyện Nhơn Hoài, Bình Định 2020-2021
- Đề thi HSG Toán 7 huyện Thái Thụy, Thái Bình 2020-2021
- Đề thi HSG Toán 7 huyện Tiền Hải, Thái Bình 2020-2021 có đáp án
- Đề thi HSG Toán 7 huyện Yên Thành, Nghệ An 2020-2021 có đáp án
- Đề thi HSG Toán 7 thành phố Bắc Giang 2020-2021
- Đề thi HSG Toán 7 trường THCS Anh Sơn, Nghệ An 2020-2021
- Đề thi chọn HSG Toán lớp 7 huyện Anh Sơn, Nghệ An qua các năm
- Đề thi HSG Toán 7 huyện Thuận Thành, Bắc Ninh 2020-2021
- Đề thi HSG Toán 7 trường THCS Anh Sơn, Nghệ An 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Lục Nam, Bắc Giang 2019-2020
- Đề thi học sinh giỏi Toán lớp 7 huyện Xuân Trường 2018-2019 có đáp án
- 500 đề thi học sinh giỏi môn Toán lớp 7 từ internet
- Đề thi Olympic Toán lớp 7 huyện Nghĩa Đàn 2018 – 2019
- 20 đề thi học sinh giỏi Toán 7 cấp huyện có đáp án
- Đề thi học sinh giỏi Toán lớp 7 số 1
- Đề thi học sinh giỏi Toán lớp 7 số 2
- Đề thi học sinh giỏi Toán lớp 7 số 3
- Đề thi học sinh giỏi Toán lớp 7 số 5
- Đề thi học sinh giỏi Toán lớp 7 huyện Lục Ngạn, Bắc Giang 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Thường Tín 2018-2019 có đáp án
- Đề thi giao lưu Olympic môn Toán 7 huyện Kinh Môn 2018-2019
- Đề thi HSG Toán 7 huyện Lục Nam 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Yên Mỹ 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Hòa Vang 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Thạch Thành 2018-2019
- Đề thi học sinh giỏi Toán lớp 7 huyện Nông Cống 2018-2019
- Đề thi Olympic Toán lớp 7 huyện Tân Thành 2017-2018
Đề thi giao lưu Olympic cấp huyện môn Toán lớp 7 huyện Kinh Môn, tỉnh Hải Dương năm học 2018-2019.
Thời gian làm bài: 150 phút.
Câu 1: (2,0 điểm)
1) Tính ![]()
2) Tính
![]() ;
;
![]() .
.
Tính ![]()
Câu 2: (2,0 điểm)
1) Tìm các cặp số nguyên (x,y) thỏa mãn: x + 2y = 3xy + 3
2) Chứng minh rằng với n nguyên dương thì 3n+2 – 2n+2 + 3n – 2n chia hết cho 10.
Câu 3: ( 2,0 điểm )
1) Cho các số dương a,b,c,d; c ≠ d và ![]() . CMR
. CMR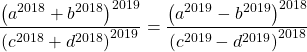
2) Cho biết ![]() .
.
Tính giá trị biểu thức: A = (3x – y – z)2019
Câu 4: (3,0 điểm)
Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao của CD và BE, K là giao của AB và DC.
1) Chứng minh rằng: DC = BE.
2) Gọi M và N lần lượt là trung điểm của CD và BE. Tính số đo góc BIK, góc AMN.
3) Chứng minh rằng IA là phân giác của góc DIE.
Câu 5 (1,0 điểm)
Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
ab+bc+ca![]()
![]() < 2(ab+bc+ca)
< 2(ab+bc+ca)
