Đề thi HK1 Toán lớp 10 THPT Nguyễn Thị Minh Khai tỉnh Đăk Lăk 2016 – 2017
Đề kiểm tra học kì 1 môn Toán lớp 10 trường THPT Nguyễn Thị Minh Khai tỉnh Đăk Lăk, năm học 2016 – 2017. Có đáp án.
Thời gian: 90 phút. (Không kể thời gian giao đề).
Hình thức thi tự luận.
A. PHẦN CHUNG (7,0 điểm):
Bài 1: (1,0 điểm) Cho các tập hợp A = {0;1; 3; 4; 5}, B = {3; 5; 6; 8; 9}.
Xác định các tập hợp A∩B, A∪B.
Bài 2: (2,0 điểm)
a) Xác định các hệ số a và b biết đường thẳng y = ax + b đi qua 2 điểm A(1; 3) và B(3; 7).
b) Vẽ đồ thị hàm số y = – x2 + 2x + 3.
Bài 3: (2,0 điểm) Giải phương trình:
a) ![]() ;
;
b) ![]() .
.
Bài 4: (2,0 điểm) Trong mặt phẳng Oxy, cho A(1; -2), B(4; 2) và C(5; 1).
a) Tìm tọa độ của vectơ ![]() ; Tính
; Tính ![]() ;
;
b) Tính ![]() .
.
B. PHẦN RIÊNG (3,0 điểm): Học sinh chỉ làm phần dành cho lớp mình.
1. Phần dành cho lớp 10A, 10B
Bài 5a: (2,0 điểm)
1) Giải hệ phương trình (không sử dụng máy tính bỏ túi):
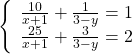
2) Cho a, b, c > 0 thoả mãn ![]() . Tìm GTNN của biểu thức:
. Tìm GTNN của biểu thức:
![]() .
.
Bài 6a: (1,0 điểm) Cho tam giác ABC vuông tại A, có ![]() và cạnh
và cạnh ![]() . Tính giá trị các biểu thức sau:
. Tính giá trị các biểu thức sau:
1) ![]() ;
;
2) ![]() .
.
2. Phần dành cho các lớp 10C, 10D,10E, 10G
Bài 5b: (2,0 điểm)
1) Giải hệ phương trình: ![]() (không sử dụng máy tính bỏ túi)
(không sử dụng máy tính bỏ túi)
2) Cho ![]() là các số dương.. Chứng minh rằng:
là các số dương.. Chứng minh rằng:
![]() .
.
Bài 6b: (1,0 điểm) Cho hình vuông ABCD có cạnh a. Tính giá trị các biểu thức sau:
1) ![]() ;
;
2) ![]() .
.
Đáp án đề kiểm tra HK1 Toán 10 THPT Nguyễn Thị Minh Khai 2016 – 2017
| Bài | Nội dung | Điểm | |
| Bài 1 (1 điểm) | (1đ) | 2×0,5 | |
| Bài 2 (2 điểm)
| a) (1đ) | 2×0,5 | |
| b) (1đ) | Đỉnh I(1;4) Trục đối xứng x=1 Vẽ đúng đồ thị | 2×0,25 0,5 | |
| Bài 3 (2 điểm) | a) (1đ) | Điều kiện
Vậy pt có 2 nghiệm x=1, x=3 | 4×0,25 |
| b) (1đ) | Nếu
Nếu
Vậy pt có 1 nghiệm x=4 | 2×0,5 | |
| Bài 4 (2 điểm) | a) | 2×0,5 | |
| b) | 1,0 | ||
| Bài 5a (2 điểm) | 1) (1đ) | 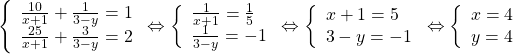 Hệ PT có nghiệm (4;4) | 4×0,25 |
| 2) (1đ) | Áp dụng bất đẳng thức cô-si , Ta có: 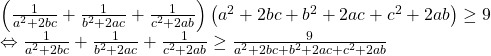 Do đó P = Vậy Min P=9 | 2×0,5 |
| Bài 6a (1 điểm) | 1) | Ta có
| 2×0,25
|
| 2) | 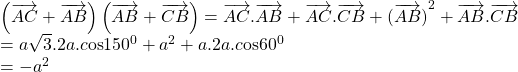 | 0,5 | |
| Bài 5b (2 điểm) | 1) (1đ) | 1,0 | |
| 2) (1đ) | Ta có:
Do đó
| 4×0,25 | |
| Bài 6b (1 điểm) |
| 0,5 0,5
|
Lưu ý: Học sinh có thể giải bằng các cách khác nếu đúng vẫn cho điểm tối đa tương ứng với thang điểm của ý và câu đó.
Đề thi Toán 10 - Tags: đề kiểm tra hk1 toán 10, đề kiểm tra học kì 1, đề thi hk1 toán 10, tỉnh Đắk Lắk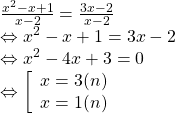
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}a+b+c+d\ge 4\sqrt[4]{{abcd}}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\ge 4\sqrt[4]{{\frac{1}{{abcd}}}}\end{array}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-d0b8a050b229787c0b9d2ff0b6cf9744_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}(a+b+c+d)\left( {\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \right)\ge 4\sqrt[4]{{abcd}}.4\sqrt[4]{{\frac{1}{{abcd}}}}\\\Leftrightarrow (a+b+c+d)\left( {\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \right)\ge 16\\\Leftrightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\ge \frac{{16}}{{a+b+c+d}}\end{array}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-1374e66118b32e1cd28b4b06f05d5c2d_l3.png)
