Ví dụ tìm điều kiện xác định của biểu thức chứa căn
Hướng dẫn học sinh lớp 9 tìm điều kiện xác định của biểu thức chứa căn thức qua các ví dụ có lời giải chi tiết.
Đây là dạng toán cơ bản mà học sinh phải nắm vững.
Ghi nhớ
+ Hàm số ![]() xác định ⇔
xác định ⇔ ![]() .
.
+ Hàm phân thức xác định ⇔ mẫu thức khác 0.
Ví dụ
Ví dụ 1: Tìm điều kiện của x để các biểu thức sau có nghĩa:
a) ![]()
b) ![]()
c) ![]()
Giải:
a) ![]() xác định ⇔
xác định ⇔ ![]()
b) ![]() xác định ⇔
xác định ⇔ ![]()
c) ![]() xác định
xác định
![]()
![]()
Ví dụ 2: Tìm điều kiện xác định của các biểu thức sau:
a) ![]()
b) ![]()
c) ![]()
Giải:
a) ![]() xác định
xác định
![]()
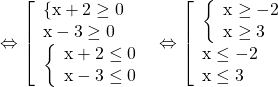
![]()
Vậy điều kiện xác định của biểu thức là ![]() hoặc
hoặc ![]() .
.
b) ![]() xác định
xác định
![]()
![]()
![]()
![]()
![]() (vì
(vì ![]() )
)
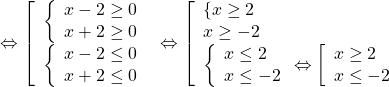
Vậy điều kiện xác định của biểu thức là ![]() hoăc
hoăc ![]() .
.
c) ![]() xác định
xác định
![]()
![]()
Vậy điều kiện xác định của biểu thức là ![]() .
.
Một số ví dụ vẽ đồ thị hàm số bậc nhất y=ax+b
Khảo sát và vẽ đồ thị hàm số bậc hai y=ax^2
Cách vẽ đồ thị hàm số bậc nhất y=ax+b
5 bài tập giải hệ PT bằng phương pháp cộng đại số có lời giải
Giải hệ phương trình bằng phương pháp thế
Giải bài toán bằng cách lập hệ phương trình
Chuyên đề Hàm số bậc nhất – Đại số 9
