Cách giải dạng toán chia hết nâng cao lớp 6
- Các bài toán nâng cao về tập hợp số tự nhiên – Số học 6
- Sách Toán nâng cao và các chuyên đề Toán 6
- Cách giải dạng toán chia hết nâng cao lớp 6
- 32 bài tập cơ bản và nâng cao Số học 6 có đáp án
- Một số bài toán nâng cao lớp 6 có lời giải
- Phương pháp tính tổng dãy số lũy thừa có quy luật
- Các dạng toán Tính tổng dãy số lũy thừa có quy luật
- Một số bài tập nâng cao Số học 6
- Dạng bài tập rút gọn nâng cao lớp 6 có hướng dẫn giải
- Dạng bài tập Tính tổng tự nhiên nâng cao lớp 6 có hướng dẫn giải
- Dạng bài tập Tính tổng phân số nâng cao lớp 6 có hướng dẫn giải
Để giải dạng toán chia hết trong chương trình Toán nâng cao lớp 6 các em cần nắm rõ tính chất chia hết, cách phân tích cấu tạo số.
Trước tiên cần nhớ lại dấu hiệu chia hết của một số:
Dấu hiệu chia hết
– Dấu hiệu chia hết cho 2: Những số chẵn có tận cùng là 0; 2; 4; 6; 8.
– Dấu hiệu chia hết cho 3: Những số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
– Dấu hiệu chia hết cho 9: Những số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
– Dấu hiệu chia hết cho 5: Những số chẵn có tận cùng là 0 hoặc 5.
Và ghi nhớ thêm:
Các số hạng cùng chia hết cho 2; 3; 5; 9 thì tổng của các số đó cũng chia hết cho 2; 3; 5; 9. Tức là:
a và b chia hết cho 2; 3; 5; 9 thì a + b cũng chia hết 2; 3; 5; 9
* Chú ý: Điều ngược lại chưa chắc đúng (không được áp dụng).
Phương pháp giải dạng toán chia hết
Ví dụ 1:
a) Chứng minh ![]() ;
; ![]()
b) Chứng minh ![]()
![]()
![]()
![]()
![]()
c) Chứng minh ![]() . Chứng minh
. Chứng minh ![]() chia hết cho 7.
chia hết cho 7.
d) Chứng minh rằng: nếu ![]() thì
thì ![]() .
.
Giải:
a) ![]()
![]()
![]()
Nhận thấy: ![]() có tận cùng là 1 nếu n chẵn và tận cùng là 9 nếu n lẻ
có tận cùng là 1 nếu n chẵn và tận cùng là 9 nếu n lẻ
![]() có tận cùng là số 1
có tận cùng là số 1 ![]() có tận cùng là 3
có tận cùng là 3
b)
Nhận thấy: ![]() có tận cùng là 8
có tận cùng là 8 ![]() có tận cùng là 4
có tận cùng là 4 ![]() có tận cùng là 2
có tận cùng là 2
![]() có tận cùng là 3 + 2 = 5.
có tận cùng là 3 + 2 = 5.
Vậy ![]()
![]()
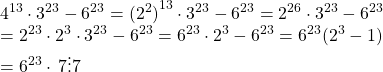
![]()
Nhận thấy: ![]() có tận cùng là 1 nếu n chẵn và tận cùng là 9 nếu n lẻ
có tận cùng là 1 nếu n chẵn và tận cùng là 9 nếu n lẻ
![]() có tận cùng là 9
có tận cùng là 9
![]() có tận cùng là 10 nên chia hết cho 10.
có tận cùng là 10 nên chia hết cho 10.
c)
![]()
Do ![]()
Nên ![]() (đpcm)
(đpcm)
d)
![]()
Mà ![]() (đpcm)
(đpcm)
Bài 7: Cho ![]()
a) Chứng minh rằng: A chia hết cho 3, cho 6
b) Tìm chữ số tận cùng của A.
Giải:
a)
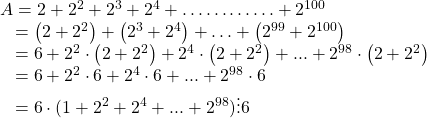
A chia hết cho 6 nên A chia hết cho 3 và 2.
b)
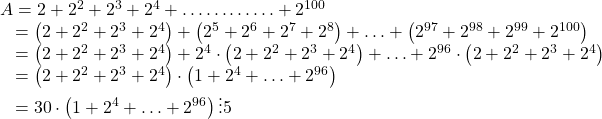
A chia hết cho 2 và 5 nên chia hết cho 10.
Vậy A có tận cùng là 0.
Số học 6 - Tags: chia hết, toán 6, toán nâng cao