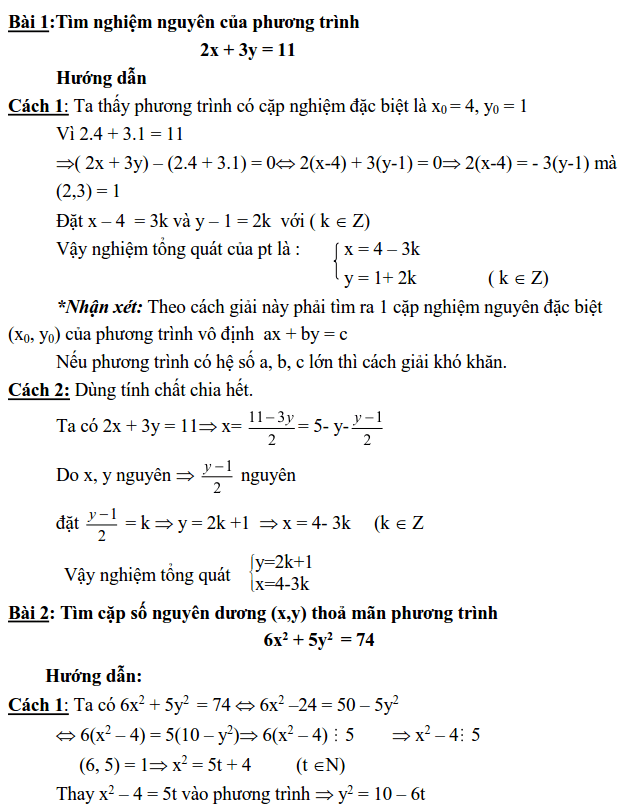Cách giải phương trình nghiệm nguyên
Chuyên đề phương trình nghiệm nguyên là một trong những chuyên đề bồi dưỡng học sinh giỏi ở cấp 2 dành cho học sinh khá giỏi.
Ở bài viết này, Gia sư Tiến Bộ chia sẻ với các em một số phương pháp thường dùng để giải tìm nghiệm nguyên của phương trình.
Các phương pháp giải phương trình nghiệm nguyên:
* Chú ý: Tùy từng bài mà các em áp dụng một hay kết hợp nhiều phương pháp để giải bài toán PT nghiệm nguyên.
1. Sử dụng tính chẵn lẻ để giải PT nghiệm nguyên
Ví dụ 1: Tìm x, y nguyên tố thoả mãn: y2 – 2x2 = 1
Hướng dẫn:
Ta có y2 – 2x2 = 1 ⇒ y2 = 2x2 +1 ⇒ y là số lẻ
Đặt y = 2k + 1 (với k nguyên).Ta có (2k + 1)2 = 2x2 + 1
⇔ x2 = 2 k2 + 2k ⇒ x chẵn , mà x nguyên tố ⇒ x = 2, y = 3
Ví dụ 2: Tìm nghiệm nguyên dương của phương trình: (2x + 5y + 1)(2|x| + y + x2 + x) = 105
Hướng dẫn:
Ta có: (2x + 5y + 1)(2|x| + y + x2 + x) = 105
Ta thấy 105 lẻ ⇒ 2x + 5y + 1 lẻ ⇒ 5y chẵn ⇒ y chẵn
2|x| + y + x2 + x = 2|x| + y + x(x+ 1) lẻ
có x(x+ 1) chẵn, y chẵn ⇒ 2|x| lẻ ⇒ 2|x| = 1 ⇒ x = 0
Thay x = 0 vào phương trình ta được
(5y + 1) ( y + 1) = 105 ⇔ 5y2 + 6y – 104 = 0
⇒ y = 4 hoặc y = ![]() ( loại)
( loại)
Thử lại ta có x = 0; y = 4 là nghiệm của phương trình
2. Dùng cách phân tích để giải PT nghiệm nguyên
Thực chất là biến đổi phương trình về dạng:
g1 (x1, x2,…., xn) h (x1, x2,…., xn) = a
Ví dụ 3: Tìm nghiệm nguyên của phương trình: x4 + 4x3+ 6x2+ 4x = y2
Hướng dẫn: Ta có: x4 + 4x3+ 6x2+ 4x = y2 ⇔ x4 +4x3+6x2+4x +1- y2=1
⇔ (x+1)4 – y2 = 1 ⇔ [(x+1)2 –y] [(x+1)2+y]= 1
⇔ ![]() hoặc
hoặc ![]()
![]()
⇒ y = 0 ⇒ (x+1)2 = 1 ⇔ x+1 = ±1 ⇒ x = 0 hoặc x = -2
Vậy ( x, y ) = ( 0, 0 ); ( – 2, 0 )
3. Dùng phương pháp cực hạn để giải PT nghiệm nguyên
Sử dụng đối với 1 số bài toán vai trò của các ẩn bình đẳng như nhau:
Ví dụ 4: Tìm nghiệm nguyên dương của phương trình:
5 ( x + y + z + t ) + 10 = 2 xyzt
Hướng dẫn:
Ta giả sử x ≥ y ≥ z ≥ t ≥ 1
Ta có: 5 ( x + y + z + t ) + 10 = 2 xyzt
⇔ ![]() hoặc
hoặc ![]()
* Với ![]() ta có
ta có ![]() xyz
xyz
![]()
Nếu ![]() có
có ![]()
⇔ ![]() hoặc
hoặc ![]()
Ta được nghiệm ( 35; 3; 1; 1); (9; 5; 1; 1) và các hoán vị của chúng
Với ![]() phương trình không có nghiệm nguyên
phương trình không có nghiệm nguyên
* Với ![]() thì
thì ![]()
![]()
Do x ≥ y ≥ z ≥ 2 nên 8x – 5 ≥ 8y – 5 ≥ 11
⇒ (8x – 5) (8y – 5) = 265 vô nghiệm
vậy nghiệm của phương trình là bộ (x, y, z)
= ( 35; 3; 1; 1); (9; 5; 1; 1) và các hoán vị
4. Phương pháp loại trừ để giải PT nghiệm nguyên
Khẳng định nghiệm rồi loại trừ các giá trị còn lại của ẩn.
Ví dụ 5: Tìm nghiệm nguyên dương của phương trình
1! + 2! + … + x! = y2
Hướng dẫn:
Với x ≥ 5 thì x! có tận cùng là 0 và 1! + 2! + 3! + 4! Có tận cùng là 3
Þ 1! + 2! + … + x! có tận cùng là 3, không là số chính phương (loại)
Vậy x < 5 mà x nguyên dương nên: x = {1;2;3;4}
Thử vào phương trình ta được (x = 1, y= 2); (x = 3, y= 3) là thoả mãn.
Ví dụ 6: Tìm tất cả các nghiệm nguyên của phương trình: y2 + y = x4 + x3 + x2 + x
Hướng dẫn:
Ta có : y2 + y = x4 + x3 + x2 + x ⇔ 4 y2+4y+1=4 x4 + 4 x3 + 4x2 + 4x+1
⇒ (2x2 + x ) 2 – (2y + 1)2 = (3x + 1) (x +1)
hay (2x2 + x + 1) 2 – (2y+ 1)2 = x(x-2)
Ta thấy:
Nếu x> 0 hoặc x< – 1 thì (3x + 1) (x +1) > 0
Nếu x > 2 hoặc x < -1 thì x (x-2) > 0
⇒ Nếu x>2 hoặc x< 1 thì (2x2 + x) <(2y+1)2 < (2x2 + x + 1) 2 (loại)
⇒ -1 ≤ x ≤ 2 ⇒ x = 0, 1, -1, 2
Xét x = 2 ⇒ y2 + y =30 ⇒ y = 5 hoặc y= -6
Xét x= 1 ⇒ y2 + y = 4 (loại)
Xét x = 0 ⇒ y2 + y = 0 ⇒ y (y + 1) = 0 ⇒ y = 0 hoặc y = -1
Xét x = -1 ⇒ y2 + y = 0 ⇒ y = 0 hoặc y= -1
Vậy nghệm nguyên của phương trình là:
(x,y) = (2, 5); (2, -6); (0, 0); (0, -1); (-1;0); (-1, -1)
5. Dùng chia hết và có dư để giải PT nghiệm nguyên
Ví dụ 7: Tìm nghiệm nguyên của phương trình: x2 – 2y2 = 5
Hướng dẫn:
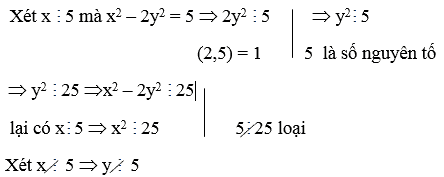
và x2 chia cho 5 có các số dư 1 hoặc 4
y2 chia cho 5 có các số dư 1 hoặc 4 ⇒ 2y2 chia cho 5 dư 2 hoặc 3
⇒ x2 – 2 y2 chia cho 5 dư ±1 hoặc ±2 (loại)
Vậy phương trình x2 – 2y2 = 5 vô nghiệm.
Ví dụ 8: Tìm x, y là số tự nhiên thoả mãn
x2 + 3y = 3026
Hướng dẫn:
Xét y = 0 ⇒ x2 + 30 = 3026 ⇒ x2 = 3025
mà xº ∈ N ⇒ x = 55
Xét y > 0 ⇒ 3y chia hết cho 3, x2 chia cho 3 dư 0 hoặc 1
⇒ x2 + 3y chia cho 3 dư 0 hoặc 1
mà 3026 chia cho 3 dư 2 (loại)
Vậy nghiệm (x,y) = (55,0)
6. Sử dụng tính chất của số nguyên tố để giải PT nghiệm nguyên
Ví dụ 9: Tìm x, y, z nguyên tố thoả mãn: xy + 1 = z
Hướng dẫn:
Ta có x, y nguyên tố và xy + 1 = z ⇒ z > 3
Mà z nguyên tố ⇒ z lẻ ⇒ xy chẵn ⇒ x chẵn ⇒ x = 2
Xét y = 2 ⇒ 22 + 1 = 5 là nguyên tố ⇒ z = 5 (thoả mãn)
Xét y> 2 ⇒ y = 2k + 1 (k ∈ N) ⇒ 22k+1 + 1 = z ⇒ 2. 4k + 1 = z
Có 4 chia cho 3 dư 1 ⇒ (2.4k+1) chia hết cho 3 ⇒ z chia hết cho 3 không thỏa mãn (loại)
Vậy x = 2, y = 2, z = 5 thoả mãn
7. Đưa về dạng tổng để giải PT nghiệm nguyên
Ví dụ 10: Tìm nghiệm nguyên của phương trình: x2 + y2 – x – y = 8
Hướng dẫn:
Ta có x2 + y2 –x – y = 8 ⇒ 4 x2 + 4 y2 – 4 x –4y = 32
⇔ (4x2 – 4x +1) + (4y2 – 4y + 1) = 34 ⇔ (2x – 1)2 + (2y – 1)2 = 34
Bằng phương pháp thử chọn ta thấy 34 chỉ có duy nhất 1 dạng phân tích thành tổng của 2 số chính phương 32 và 52
Do đó ta có ![]() hoặc
hoặc ![]()
Giải ra ta được (x,y) = (2,3); (2,-2); (-1, -2); (-1, 3) và các hoán vị của nó.
Ví dụ 11: Tìm nghiệm nguyên của phương trình
x2 – 4xy + 5y2 = 169
Hướng dẫn: Ta có x2 – 4xy + 5y2 = 169 ⇔ (x – 2y)2 + y2 = 169
Ta thấy 169 = 02 + 132 = 52 + 122
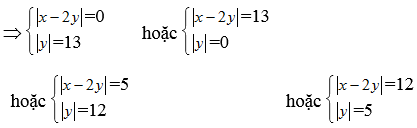
Giải ra ta được (x, y) = (29, 12);(19, 12); (-19, -12); (22, 5); (-2, 5) ;(2, -5); (-22, -5); (26, 13); (-26, -13); (-13. 0); (13, 0)
8. Dùng phương pháp lùi vô hạn để giải PT nghiệm nguyên
Ví dụ 12: Tìm nghiệm nguyên của phương trình: x2 – 5y2 = 0
Hướng dẫn:
Giả sử x0, y0 là nghiệm của phương trình x2 – 5y2 = 0
ta có ![]() đặt
đặt ![]()
Ta có ![]()
![]() dăt
dăt ![]()
Vây nếu (xo;yo) là nghiệm của phương trình đã cho thì ![]() cũng là nghiệm của phương trình đã cho. Cứ tiếp tục lập luận như vậy
cũng là nghiệm của phương trình đã cho. Cứ tiếp tục lập luận như vậy ![]() với k nguyên dương bất kỳ cũng là nghiệm của phương trình. Điều này xảy ra khi
với k nguyên dương bất kỳ cũng là nghiệm của phương trình. Điều này xảy ra khi ![]()
Vậy phương trình có nghiệm duy nhất là x = y = 0.
Ví dụ 13: Tìm nghiệm nguyên của phương trình: x2 + y2 + z2 = x2 y2
Hướng dẫn:
Nếu x, y đều là số lẻ ⇒ x2 , y2 chia cho 4 đều dư 1
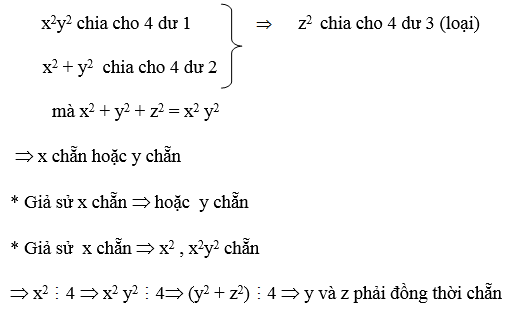
Đặt x = 2x1, y = 2y1, z = 2z1
Ta có x+ y+z = xy
lập luận tương tự ta có x + y + z = 16 xy
Quá trình này cứ tiếp tục ta thấy (x1, y1, z1 ) là nghiệm của phương trình thì
![]() là nghiệm của phương trình với k nguyên dương
là nghiệm của phương trình với k nguyên dương
⇒ x1 = y1 = z1 = 0
Vậy phương trình có nghiệm là (0, 0, 0)
9. Sử dụng tính chất nghiệm của phương trình bậc 2 để giải PT nghiệm nguyên
Biến đổi phương trình về dạng phương trình bậc 2 của ẩn coi các ẩn khác là tham số, sử dụng các tính chất về nghiệm của phương trình bậc 2 để xác định giá trị của tham số.
Ví dụ 14: Giải phương trình nghiệm nguyên: 3x2 + y2 + 4xy + 4x + 2y + 5 = 0
Hướng dẫn:
Ta có PT: 3x2 + y2 + 4xy + 4x + 2y + 5 = 0
⇒ y2 + (4x + 2)y + 3 x2 + 4x + 5 = ) (*) coi x là tham số giải phương trình bậc 2 pt (*) ẩn y ta có
![]()
Do y nguyên, x nguyên ![]() nguyên
nguyên
Mà ![]()
⇒ (x- n) (x+ n) = 4 ⇒ x – n = x + n = ± 2 ⇒ x = ± 2
Vậy phương trình có nghiệm nguyên
(x, y) = (2; -5); (-2, 3)
Ví dụ 15: Tìm nghiệm nguyên của phương trình: x2 – (y+5)x + 5y + 2 = 0
Hướng dẫn:
Ta có x2 – (y+5)x + 5y + 2 = 0 coi y là tham số ta có phương trình bậc 2 ẩn x. Giả sử phương trình bậc 2 có 2 nghiệm x1, x2
Ta có: ![]()
⇒ ![]()
⇒ 5 x1 + 5x2 – x1x2 = 23
⇔ (x1 -5) (x2 -5) = 2 Mà 2 = 1.2 = (-1)(-2)
⇒ x1 + x2 = 13 hoặc x1 + x2 = 7 ⇒ y = 8 hoặc y = 2
thay vào phương trình ta tìm được các cặp số
(x,y ) = (7, 8); (6, 8); (4, 2); (3, 2); là nghiệm của phương trình
10. Dùng bất đẳng thức để giải PT nghiệm nguyên
Ví dụ 16: Tìm nghiệm nguyên của phương trình: x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- ![]() )2 = 3 –
)2 = 3 – ![]()
Ta thấy (x- ![]() )2 = 3 –
)2 = 3 – ![]() ≥ 0
≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)
Bài tập phương trình nghiệm nguyên có lời giải: