Điều kiện cần và đủ để hàm số có cực trị
1. Điều kiện cần để hàm số có cực trị
Định lí 1. Giả sử hàm số ![]() có đạo hàm tại điểm
có đạo hàm tại điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Điều kiện đủ để hàm số có cực trị
Định lí 2.
Giả sử hàm số ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Có thể không có đạo hàm tại
(Có thể không có đạo hàm tại ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
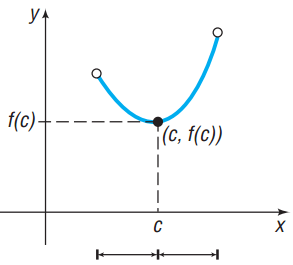
– Nếu ![]() đổi dấu từ âm sang dương khi
đổi dấu từ âm sang dương khi ![]() qua điểm
qua điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
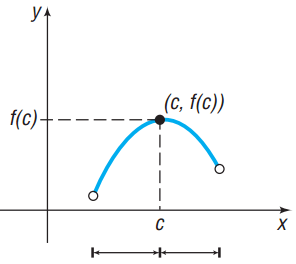
– Nếu ![]() đổi dấu từ dương sang âm khi
đổi dấu từ dương sang âm khi ![]() qua điểm
qua điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Minh họa bằng đồ thị
| Hàm số
| Hàm số
|
Định lí 3.
Giả sử hàm số ![]()
![]()
![]()
![]()
![]()
![]() chứa điểm
chứa điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Khi đó:
. Khi đó:
– Nếu ![]() thì hàm số đạt cực đại tại điểm
thì hàm số đạt cực đại tại điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
– Nếu ![]() thì hàm số đạt cực tiểu tại điểm
thì hàm số đạt cực tiểu tại điểm ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()