Các dạng bài tập Đại số 8 nâng cao thường gặp
- Các dạng bài tập Đại số 8 nâng cao thường gặp
- Sách Nâng cao và phát triển Toán 8 – Vũ Hữu Bình
- Bài tập nâng cao và một số chuyên đề Toán 8 – Bùi Văn Tuyên
- Bài tập hình học chương 3 nâng cao
Các dạng bài tập Đại số 8 nâng cao thường gặp: Nhân chia đa thức, hằng đẳng thức, phân tích đa thức thành nhân tử, phép tính phân thức.
Các dạng toán nâng cao Đại số 8 bao gồm:
A. Nhân đa thức
1. Tính giá trị:
B = x15 – 8x14 + 8x13 – 8x12 + … – 8x2 + 8x – 5 với x = 7
2. Cho ba số tự nhiên liên tiếp. Tích của hai số đầu nhỏ hơn tích của hai số sau là 50. Hỏi đã cho ba số nào?
3. Chứng minh rằng nếu: ![]() thì
thì
(x2 + y2 + z2) (a2 + b2 + c2) = (ax + by + cz)2
B. Chia đa thức
1. Xác định a để cho đa thức x3 – 3x + a chia hết cho (x – 1)2
2. Tìm các giá trị nguyên của n để ![]() là số nguyên
là số nguyên
3. Tìm dư trong phép chia đa thức:
a. x – 1
b. x2 – 1
c. x2 + x + 1
4. Xác định các số a va b sao cho:
a. x4 + ax2 + b chia hết cho:
i. x2 – 3x + 2
ii. x2 + x + 1
b. x4 – x3 – 3x2 + ax + b chia cho x2 – x – 2 có dư là 2x – 3
c. 2x2 + ax + b chia cho x + 1 dư – 6 chia cho x – 2 dư 21
2. Chứng minh rằng
f(x) = (x2 – x + 1)1994 + (x2 + x – 1)1994 – 2
chia hết cho x – 1. Tìm dư trong phép chia f(x) cho x2 – 1
3. Tìm n nguyên để ![]() là số nguyên
là số nguyên
4. Chứng minh rằng:
a. 1110 – 1 chia hết cho 100
b. 9 . 10n + 18 chia hết cho 27
c. 16n – 15n – 1 chia hết cho 255
5. Tìm tất cả các số tự nhiên n để 2n – 1 chia hết cho 7
6. Chứng minh rằng:
a. 20n + 16n – 3n – 1:323 với n chẵn
b. 11n + 2 + 122n + 1:133
c. ![]() chia hết cho 7 với n > 1
chia hết cho 7 với n > 1
C. Hằng đẳng thức
1. Rút gọn các biểu thức sau:
a. A = 1002 – 992 + 982 – 972 + … + 22 – 12
b. B = 3(22 + 1) (24 + 1) … (264 + 1) + 1
c. C = (a + b + c)2 + (a + b – c)2 – 2(a + b)2
2. Chứng minh rằng:
a. a3 + b3 = (a + b)3 – 3ab (a + b)
b. a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 c2 – ab – bc – ca)
Suy ra các kết quả:
i. Nếu a3 + b3 + c3 = 3abc thì a + b + c = 0 hoặc a = b = c
ii. Cho ![]() tính
tính ![]()
iii. Cho a3 + b3 + c3 = 3abc (abc ≠ 0)
Tính ![]()
3. Tìm giá trị nhỏ nhất của các biểu thức
a. A = 4x2 + 4x + 11
b. B = (x – 1) (x + 2) (x + 3) (x + 6)
c. C = x2 – 2x + y2 – 4y + 7
4. Tìm giá trị lớn nhất của các biểu thức
a. A = 5 – 8x – x2
b. B = 5 – x2 + 2x – 4y2 – 4y
5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c
b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0
6. Chứng minh rằng:
a. x2 + xy + y2 + 1 > 0 với mọi x, y
b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z
7. Chứng minh rằng:
x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
8. Tổng ba số bằng 9, tổng bình phương của chúng bằng 53. Tính tổng các tích của hai số trong ba số ấy.
9. Chứng minh tổng các lập phương của ba số nguyên liên tiếp thì chia hết cho 9.
10. Rút gọn biểu thức:
A = (3 + 1) (32 + 1) (34 + 1) … (364 + 1)
11. a. Chứng minh rằng nếu mỗi số trong hai số nguyên là tổng các bình phương của hai số nguyên nào đó thì tích của chúng có thể viết dưới dạng tổng hai bình phương.
b. Chứng minh rằng tổng các bình phương của k số nguyên liên tiếp (k = 3, 4, 5) không là số chính phương.
D. Phân tích đa thức thành nhân tử
1. Phân tích đa thức thành nhân tử:
a. x2 – x – 6
b. x4 + 4x2 – 5
c. x3 – 19x – 30
2. Phân tích thành nhân tử:
a. A = ab(a – b) + b(b – c) + ca(c – a)
b. B = a(b2 – c2) + b(c2 – a2) + c(a2 – b2)
c. C = (a + b + c)3 – a3 – b3 – c3
3. Phân tích thành nhân tử:
a. (1 + x2)2 – 4x (1 – x2)
b. (x2 – 8)2 + 36
c. 81x4 + 4
d. x5 + x + 1
4. a. Chứng minh rằng: n5 – 5n3 + 4n chia hết cho 120 với mọi số nguyên n.
b. Chứng minh rằng: n3 – 3n2 – n + 3 chia hết cho 48 với mọi số lẻ n.
5. Phân tích các đa thức sau đây thành nhân tử
a. a3 – 7a – 6
b. a3 + 4a2 – 7a – 10
c. a(b + c)2 + b(c + a)2 + c(a + b)2 – 4abc
d. (a2 + a)2 + 4(a2 + a) – 12
e. (x2 + x + 1) (x2 + x + 2) – 12
f. x8 + x + 1
g. x10 + x5 + 1
6. Chứng minh rằng với mọi số tự nhiên lẻ n:
a. n2 + 4n + 8 chia hết cho 8
b. n3 + 3n2 – n – 3 chia hết cho 48
7. Tìm tất cả các số tự nhiên n để :
a. n4 + 4 là số nguyên tố
b. n1994 + n1993 + 1 là số nguyên tố
8. Tìm nghiệm nguyên của phương trình:
a. x + y = xy
b. p(x + y) = xy với p nguyên tố
c. 5xy – 2y2 – 2x2 + 2 = 0
E. Phân thức
1. Tính các tổng sau
a. 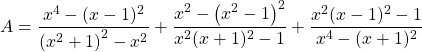
b. ![]() vói
vói ![]()
2. Cho ![]()
Chứng minh rằng: ![]()
3. Cho phân thức: ![]()
a. Chứng minh rằng nếu ![]() thì trong ba số
thì trong ba số ![]() có một số bằng tổng hai số kia và trong phân thức A có một phân thức bằng – 1 còn hai phân thức còn lại bằng 1 .
có một số bằng tổng hai số kia và trong phân thức A có một phân thức bằng – 1 còn hai phân thức còn lại bằng 1 .
b. Nếu ![]() là độ dài các đoạn thẳng và
là độ dài các đoạn thẳng và ![]() . Chứng
. Chứng ![]() là độ dài các cạnh của một tam giác.
là độ dài các cạnh của một tam giác.
4. Chứng minh rằng nếu a, b, c khác nhau đôi một thì:
a. ![]()
b. ![]() nếu
nếu ![]()
5. Chứng minh rằng nếu:
![]() và
và ![]()
Thì ![]()
6. Cho a, b, c và x, y, z là các số khác nhau và khác không chứng minh rằng
Nếu: ![]() và
và ![]() thì
thì ![]()
