Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
- Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
- Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau khi rút gọn
- Đồ thị hàm số bậc nhất và bậc hai
- Giải và biện luận phương trình bậc nhất một ẩn
- Giải và biện luận hệ phương trình bậc nhất hai ẩn
- Phương trình bậc hai – Hệ thức Vi-ét
- Cách tìm hai số khi biết tổng và tích của chúng
- Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
- Hệ phương trình bậc nhất chứa tham số
- Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
- Biện luận nghiệm của phương trình bậc 2 bằng đồ thị
- Các dạng bài tập giải bài toán bằng cách lập phương trình, hệ phương trình
- 30 bài tập hình học ôn thi vào 10 môn Toán
- Dạng bài tìm điều kiện về nghiệm của phương trình bậc hai
- Bài tập: Rút gọn biểu thức và câu hỏi phụ – Ôn thi vào 10
- Bài tập bất đẳng thức lớp 9 không chuyên
- 32 bài tập giải bài toán bằng cách lập phương trình, hệ phương trình cơ bản
- Các dạng bài tập Đại số ôn thi vào lớp 10
- Ôn thi vào 10 môn Toán năm học 2020-2021
- 5 đề thi thử vào lớp 10 THPT môn Toán năm 2021
- Đề thi thử môn Toán vào lớp 10 THPT năm 2021-2022 có lời giải
- Chuyên đề: Phương trình và hệ phương trình ôn thi vào 10
- 68 bài tập: giải toán bằng cách lập phương trình, hệ phương trình
- Một số bài hình ôn thi vào lớp 10 có lời giải
- Những bài toán hình học mẫu ôn thi HK2 và tuyển sinh vào 10 môn Toán
Gia sư Tiến Bộ chia sẻ những cách thường dùng để giải bài toán chứng minh bất đẳng thức trong đề thi tuyển sinh vào lớp 10 môn Toán.
Không có cách chung để giải mọi bài toán bất đẳng thức. Do đó tùy từng bài mà chúng ta sử dụng phương pháp giải cho phù hợp.
1. Biến đổi tương đương
Từ BĐT đề yêu cầu chứng minh, ta biến đổi đến bất đẳng thức đúng, như vậy BĐT đã được chứng minh.
Bài 1: Chứng minh ![]()
Giải
![]()
![]()
Vậy để chứng minh BĐT(1) ta phải chứng minh BĐT (2)
Nếu VP= ac + bd < 0 thì (2) đúng
Nếu ![]()
![]()
![]()
BĐT cuối luôn đúng vậy ta có ![]()
![]()
![]()
2. Sử dụng các bất đẳng thức đã biết
2.1. Sử dụng BĐT suy ra từ BĐT (a-b)2 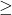 0
0
Đây là một trong các phương pháp (PP) thường ra trong các đề thi tuyển sinh vào 10
Ví dụ:
a) Từ ![]() .
.
b) Với x > 1 ta có:
![]()
![]()
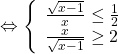
……(Người ra đề cứ lấy một BĐT bất kỳ , từ đó khai triển , kết hợp vài BĐT như vậy sẻ có bài toán của đề thi. Vì vậy người học khó chờ cơ hội trúng đề mà chỉ cần nắm chắc PP giải, biết lựa chọn BĐT xuất phát đúng ắt sẽ giải được bài). Ví dụ ta có các bài toán sau.
Bài 2: Cho 3 số ![]() thỏa mãn
thỏa mãn ![]() .
.
Chứng minh: ![]()
Giải:
![]() .
.
Tương tự ta có: ![]()
Lấy (1) +(2)+(3) được:
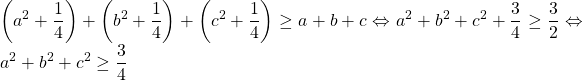
Dấu “=” khi ![]()
Bài 3: Cho x ![]() 1; y
1; y ![]() 4 . Chứng minh rằng
4 . Chứng minh rằng ![]()
Giải:
Ta có :
![]()
![]()
![]()
Ta có :
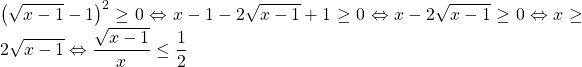 (1)
(1)
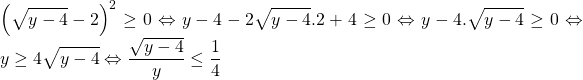 (2)
(2)
Cộng BĐT (1) với BĐT (2) theo vế được ![]()
Vậy ![]()
Dấu “=” khi ![]() và
và ![]()
2.2. Dùng BĐT Cô-Si cho hai số không âm
Với ![]() không âm ta có:
không âm ta có: ![]()
![]() . Dấu “=” khi
. Dấu “=” khi ![]()
2.2.1. Kỹ thuật 1:
Tách 1 hạng tử chứa biến thành tổng của một hằng số với 1 hạng tử chứa biến sao cho hạng tử này là nghịch đảo của 1 hạng tử khác có trong biểu thức đã cho.
Chú ý:
* 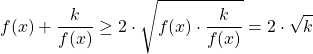
* 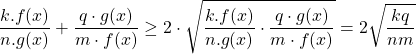
Bài 4: Cho 0 < x < 2. Chứng minh ![]()
Nhận xét: Với ĐK bài toán các biểu thức ”số hạng” đều dương ![]() khả năng dùng BĐT Cô si. Muốn dùng Cô Si với biểu thức
khả năng dùng BĐT Cô si. Muốn dùng Cô Si với biểu thức ![]() thì biểu thức “ số hạng “ thứ hai mẫu phải chứa x và tử phải chứa
thì biểu thức “ số hạng “ thứ hai mẫu phải chứa x và tử phải chứa ![]() . Ta làm nháp như sau:
. Ta làm nháp như sau:
Nháp: Xét ![]() có dạng như chú ý.
có dạng như chú ý.
Khi đó: ![]() .
.
Giải:
Xét ![]()
Khi đó: ![]()
⇔ ![]()
Do ![]() nên. Áp dụng BĐT Cô si có:
nên. Áp dụng BĐT Cô si có:
![]()
Bài 5: Cho 0 < x < 1. Chứng minh : ![]()
Giải:
![]()
Xét ![]()
![]()
⇒ ![]()
⇒ ![]()
Dấu bằng ![]()
![]()
Giải được ![]() ;
;![]()
2.2.2 Kỹ thuật 2:
Nhân và chia một biểu thức với cùng một số khác không.
Chú ý: Dạng ![]() , ta đi xét biểu thức
, ta đi xét biểu thức ![]() sau đó dùng Cô Si
sau đó dùng Cô Si
Bài 6: Với x ≥ 9. Chứng minh A= ![]()
Ta có: ![]()
Do x ≥ 9 nên x – 9 ≥ 0. Áp dụng BĐT Cô si ta có: ![]() . Suy ra:
. Suy ra:
![]()
2.2.3 Kỹ thuật dự đoán điểm rơi
Điểm rơi của BĐT là giá trị biến mà tại đó dấu “=” xảy ra
Bài 7: Cho ![]() là các số dương thỏa mãn
là các số dương thỏa mãn ![]() .
.
Chứng minh rằng ![]()
Nhận xét: Bài toán cho vai trò ![]() như nhau , nên điểm rơi khi
như nhau , nên điểm rơi khi ![]() và ta dùng bất đẳng thức Cauchy cho từng số hạng .
và ta dùng bất đẳng thức Cauchy cho từng số hạng .
– Nếu dùng cho ![]() và
và ![]() thì dấu bằng xảy ra khi
thì dấu bằng xảy ra khi ![]() (sai so với dự đoán) .
(sai so với dự đoán) .
Điểm rơi Khi ![]() thì khi đó
thì khi đó ![]() ⇒ ta phải áp dụng bất đẳng thức Cauchy cho 1-x và 2x.
⇒ ta phải áp dụng bất đẳng thức Cauchy cho 1-x và 2x.
Giải: Ta có![]() . Tương tự cho các số hạng còn lại , rồi cộng các BĐT được:
. Tương tự cho các số hạng còn lại , rồi cộng các BĐT được:
VT ![]()
![]()
2.3 Dùng bất đẳng thức Bunhiacôpky dạng phân thức
![]() . (1) Dấu đẳng thức xảy ra khi
. (1) Dấu đẳng thức xảy ra khi ![]()
Từ đây ta suy ra một bất đẳng thức rất thường sử dụng “Với x > 0, y > 0, ta có: ![]() (2) Dấu “=” xảy ra khi x = y.
(2) Dấu “=” xảy ra khi x = y.
Hai bất đẳng thức trên khi dùng phải chứng minh.(Dùng PP tương đương)
Bài 8: Cho các số thực dương x, y, z thỏa x + y + z = 4. Chứng minh rằng : ![]()
Giải:
Từ x + y + z = 4 suy ra y + z = 4 – x
Với a; b dương ta có ![]() (*)
(*)
Ta chứng minh (*) (*)
![]()
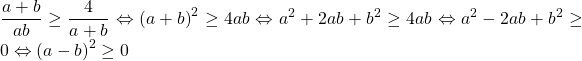
Bất đẳng thức cuối đúng nên ta có ĐPCM
Áp dụng: ![]()
Mà ![]()
Do đó: ![]()
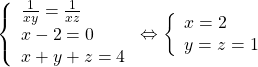
3. Phương pháp đổi biến
Bẳng cách dự đoán dấu “=” xảy ra rất nhiều bài toán BĐT ta đổi qua biến mới dễ làm hơn. Chủ yếu dùng PP tương đương sau khi đổi biến.
Bài 9: Cho ![]() . Chứng minh rằng: C =
. Chứng minh rằng: C = ![]() .
.
Nhận xét: Dự đoán đẳng thức xảy ra khi a = 1; b = 2.
Do vậy ta đặt ![]() , với
, với ![]() . Từ giả thiết suy ra
. Từ giả thiết suy ra ![]() .
.
Ta có:
![]()
= ![]() =
= ![]() (vì x ³ 0).
(vì x ³ 0).
Đẳng thức xảy ra ⇔ x = 0 hoặc x = 1 tức a = 1, b = 2 hoặc a = 0, b = 3. Vậy ![]() .
.
Bài 10: Cho ![]() . Chứng minh rằng: A =
. Chứng minh rằng: A = ![]() .
.
Nhận xét: Dự đoán rằng đẳng thức xảy ra khi a = b = c = 1.
Do vậy ta đặt: ![]() . Từ giả thiết suy ra:
. Từ giả thiết suy ra: ![]() .
.
Ta có:
![]()
= ![]()
= ![]() =
= ![]()
Đẳng thức xảy ra ⇔ y = 0 và ![]() ⇔ x = y = 0 hay
⇔ x = y = 0 hay ![]() . Vậy
. Vậy ![]() 6.
6.
Bài 11: Cho a > 1 ; b > 1 . Chứng minh: ![]()
Ở BĐT này điều kiện là bất đẳng thức. Vì a > 1và b > 1 nên ta đặt a = 1 + x; b =1+y (với x; y >0). Khi đó ta có :
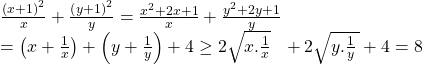
Bài 12: Cho ba số thực dương a, b, c. CMR: ![]()
Đặt: 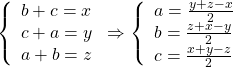
Khi đó bất đẳng thức (1) trở thành:![]()
Ta có:
![]()
![]()
Hay ![]() (đpcm)
(đpcm)
4. Phương pháp làm trội
Bổ trợ:
a)Tổng hữu hạn.
Một tổng gồm các số hạng viết theo quy luật từ số hạng đầu tiên đến số hạng cuối cùng , gọi là tổng hữu hạn.
Ví dụ: ![]() là một tổng hữu hạn.
là một tổng hữu hạn.
Để tính tổng hữu hạn ta biến đổi mỗi số hạng thành hiệu của hai số hạng.
Ví dụ: Tính A= ![]()
(Ta áp dụng công thức ![]() với a và n là số tự nhiên)
với a và n là số tự nhiên)
Ta có:
A= ![]()
![]()
b) Tích hữu hạn.
Một tích gồm các thừa số viết theo quy luật từ thừa số đầu tiên đến thừa số cuối cùng ,gọi là tích hữu hạn.
VD: ![]() là tích hữu hạn.
là tích hữu hạn.
Để tính tích hữu hạn ta biến đổi mỗi thừa số thành tich của hai thừa số.Từ vài thừa số đầu tiên ta tìm ra quy luật rút gọn.
VD: Rút gọn ![]()
Giải:
Ta có:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}B=\left( {1+\frac{1}{3}} \right)\left( {1+\frac{1}{8}} \right)\left( {1+\frac{1}{{15}}} \right)....\left( {1+\frac{1}{{{{n}^{2}}+2n}}} \right)\\B=\frac{{{{2}^{2}}}}{3}.\,\,\,\,\,\,\,\,\,\,\frac{{{{3}^{2}}}}{8}.\,\,\,\,\,\,\,\,\,\,\,\frac{{{{4}^{2}}}}{{15}}.\,\,\,\,\,\,\,..........\frac{{{{{(n+1)}}^{2}}}}{{{{n}^{2}}+2n}}=\left( {\frac{{2.2}}{{1.3}}} \right).\left( {\frac{{3.3}}{{2.4}}} \right).\left( {\frac{{4.4}}{{3.5}}} \right)........\left[ {\frac{{(n+1)(n+1)}}{{n(n+2)}}} \right]\end{array}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-e025b43f873eaed1bce3b38319de2114_l3.png)
B=![]()
a) Để Chứng minh BĐT: A > k, trong đó vế trái A là tổng(hoặc tích) hữu hạn nhưng ta không tìm được cách để tính. Ta phải biến đổi ![]() (làm trội xuống) mà A1 là tổng (hoặc tích hữa hạn) mà ta tính được.
(làm trội xuống) mà A1 là tổng (hoặc tích hữa hạn) mà ta tính được.
Bài 13: Chứng minh:
![]()
Giải:
Ta có:
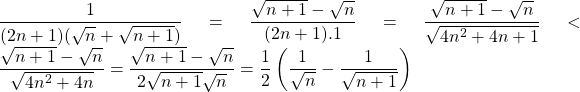 Áp dụng:
Áp dụng:
Với n = 1 có ![]()
Với n = 2 có![]()
……..
Với n = 2019 có ![]()
Cộng tất cả các BĐT được
VT < ![]()
Bài 14: CM: ![]() (Với n ∈ N và n ≠ 1)
(Với n ∈ N và n ≠ 1)
HD: Mỗi số hạng trong tổng có dạng ![]() vì CM
vì CM
VT < 2 nên ta làm trội xuống như sau:
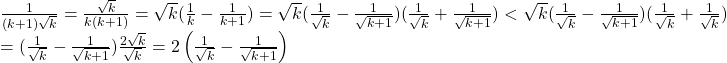
b) Để Chứng minh BĐT: B < m , trong đó vế trái B là tổng hữu hạn(hoặc tích) nhưng ta không tìm được cách để tính. Ta phải biến đổi B < B1 (làm trội lên) mà B1 là tổng (hoặc tích hữa hạn) mà ta tính được.
Bài 15: Với n là số tự nhiên và n ≥ 1. C/m :
![]()
HD: 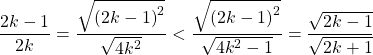
5./ Phương pháp dùng BĐT phụ để chứng minh.
Với điều kiện M ![]() P . Chứng minh A
P . Chứng minh A ![]() B.
B.
Ta chứng minh phụ sau : (A- B) + (P-M) ![]() 0 (*).
0 (*).
Lập luận : Vì P – M ![]() 0 nên
0 nên ![]() A
A ![]() B.
B.
Bài 16: Cho x2 + y2 ![]() x+y. Chứng minh : x + y
x+y. Chứng minh : x + y ![]() 2
2
Giải:
Trước hết ta chứng minh BĐT phụ sau:
(2-x-y )+ ( x2 + y2– x – y) ![]() 0
0 ![]() ( x2 – 2x +1) + (y2 – 2y +1)
( x2 – 2x +1) + (y2 – 2y +1) ![]() 0
0
![]() (x-1)2 + (y – 1)2
(x-1)2 + (y – 1)2 ![]() 0 ( BĐT đúng)
0 ( BĐT đúng)
Vì x2 + y2– x – y ![]() 0
0 ![]() 2-x-y
2-x-y ![]() 0
0 ![]() x + y
x + y ![]() 2,.Dấu “=” khi x=y = 1.
2,.Dấu “=” khi x=y = 1.
Bài 17: Cho x ; y là hai số dương thỏa : 2x+ 2y = 3 . Chứng minh : ![]()
Giải:Trước hết ta chứng minh BĐT phụ sau:
![]()
![]()
![]() . Dấu “=” khi x=1; y =
. Dấu “=” khi x=1; y = ![]()
Bài 18: Cho a+b ![]() 1 Chứng minh :
1 Chứng minh :![]()
Giải:
Trước hết ta chứng minh BĐT phụ sau:
(a2 +b2 – ![]() )+ (1-a-b) =a2 +b2 –a-b+
)+ (1-a-b) =a2 +b2 –a-b+![]() =
= ![]() BĐT đúng.
BĐT đúng.
Vì 1 –a-b ![]() 0
0 ![]()
![]()
5. Chứng minh phản chứng
Ví dụ: Cho 0 < a;b,c < 1 .CMR : có ít nhất một trong các bất đẳng thức sau là sai:
a( 1 – b) > ![]() ; b(1-c) >
; b(1-c) > ![]() , c( 1-a) >
, c( 1-a) > ![]()
Giải : Giả sử cả 3 bất đẳng thức đều đúng, nhân từng vế ta được
Þ a( 1 – b). b(1-c) c( 1-a) > ![]() (*)
(*)
mà a(1-a) = -a2 + a = -(a2 –a + ¼ -1/4 ) = -(a-1/2)2 + ¼ £ ¼ ![]() a( 1-a)
a( 1-a) ![]() (1)
(1)
tương tự b( b-1) £ ![]() (2) , c( 1-c)
(2) , c( 1-c) ![]() (3)
(3)
Lấy (1) . (2).(3) được
a(1-b) b (1-c)c(1-a) ![]()
![]() (mâu thuẫn với BĐT (*)
(mâu thuẫn với BĐT (*)
Vậy ta có ĐCCM
(GV: Lương Công Hiển-THCS Văn Lang- Vạn Ninh- Khánh Hòa)
Đại số 9 - Tags: bất đẳng thức, ôn thi vào 10, thi vào 10Ví dụ giải hệ phương trình quy về bậc nhất
Hệ phương trình bậc nhất chứa tham số
Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
Cách tìm hai số khi biết tổng và tích của chúng
Phương trình bậc hai – Hệ thức Vi-ét
Giải và biện luận hệ phương trình bậc nhất hai ẩn
Giải và biện luận phương trình bậc nhất một ẩn
