Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
- Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
- Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau khi rút gọn
- Đồ thị hàm số bậc nhất và bậc hai
- Giải và biện luận phương trình bậc nhất một ẩn
- Giải và biện luận hệ phương trình bậc nhất hai ẩn
- Phương trình bậc hai – Hệ thức Vi-ét
- Cách tìm hai số khi biết tổng và tích của chúng
- Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
- Hệ phương trình bậc nhất chứa tham số
- Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
- Biện luận nghiệm của phương trình bậc 2 bằng đồ thị
- Các dạng bài tập giải bài toán bằng cách lập phương trình, hệ phương trình
- 30 bài tập hình học ôn thi vào 10 môn Toán
- Dạng bài tìm điều kiện về nghiệm của phương trình bậc hai
- Bài tập: Rút gọn biểu thức và câu hỏi phụ – Ôn thi vào 10
- Bài tập bất đẳng thức lớp 9 không chuyên
- 32 bài tập giải bài toán bằng cách lập phương trình, hệ phương trình cơ bản
- Các dạng bài tập Đại số ôn thi vào lớp 10
- Ôn thi vào 10 môn Toán năm học 2020-2021
- 5 đề thi thử vào lớp 10 THPT môn Toán năm 2021
- Đề thi thử môn Toán vào lớp 10 THPT năm 2021-2022 có lời giải
- Chuyên đề: Phương trình và hệ phương trình ôn thi vào 10
- 68 bài tập: giải toán bằng cách lập phương trình, hệ phương trình
- Một số bài hình ôn thi vào lớp 10 có lời giải
- Những bài toán hình học mẫu ôn thi HK2 và tuyển sinh vào 10 môn Toán
Hướng dẫn cách rút gọn biểu thức chứa căn cho học sinh lớp 9. Đây là dạng toán chắc chắn có trong các đề thi tuyển sinh vào lớp 10 môn Toán.
Để giải được bài tập rút gọn và tính giá trị của biểu thức chứa căn bậc hai chúng ta cần ôn lại lý thuyết căn thức bậc hai. Tức là:
Biến đổi biểu thức chứa căn bậc hai
Vận dụng các quy tắc dưới đây:
1. Đưa thừa số ra ngoài dấu căn
Với hai biểu thức ![]() mà
mà ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Nếu ![]() và
và ![]()
![]()
![]()
![]()
![]()
![]()
Nếu ![]() và
và ![]()
![]()
![]()
![]()
![]()
![]()
2. Đưa thừa số vào trong dấu căn
Với ![]() và
và ![]()
![]()
![]()
![]()
![]()
![]()
Với ![]() và
và ![]() thì
thì ![]()
3. Khử mẫu của biểu thức lấy căn
Với hai biểu thức ![]()
![]()
![]()
![]() và
và ![]() ta có:
ta có:
![]()
4. Trục căn thức ở mẫu
Với hai biểu thức A, B mà B > 0 ta có:
![]()
Với các biểu thức ![]() mà
mà ![]() và
và ![]() ta có:
ta có:
![]()
Với các biểu thức ![]() mà
mà ![]() và
và ![]() ta có:
ta có:
![]()
Bài tập: Thực hiện phép tính chứa căn bậc hai dưới đây:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) 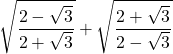 ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]()
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]()
20) ![]() .
.
Cách rút gọn biểu thức chứa căn bậc hai
Phương pháp rút gọn:
– Phân tích đa thức tử và mẫu thành nhân tử;
– Tìm ĐKXĐ (Nếu bài toán chưa cho ĐKXĐ)
– Rút gọn từng phân thức (nếu được)
– Thực hiện các phép biến đổi đồng nhất như:
+ Quy đồng (đối với phép cộng trừ) ; nhân ,chia.
+ Bỏ ngoặc: bằng cách nhân đơn ; đa thức hoặc dùng hằng đẳng thức
+ Thu gọn: cộng, trừ các hạng tử đồng dạng.
+ Phân tích thành nhân tử – rút gọn
* Chú ý: Trong mỗi bài toán rút gọn thường có các câu thuộc các loại toán: Tính giá trị biểu thức; giải Phương trình; bất phương trình; tìm giá trị của biến để biểu thức có giá trị nguyên; tìm giá trị nhỏ nhất ,lớn nhất…Do vậy ta phải áp dụng các Phương pháp giải tương ứng, thích hợp cho từng loại bài.
Ví dụ: Cho biểu thức: ![]()
a/ Rút gọn ![]() .
.
b/ Tìm giá trị của ![]() để biểu thức
để biểu thức ![]() có giá trị nguyên.
có giá trị nguyên.
Giải:
a/ Rút gọn ![]() :
:
– Phân tích: ![]()
– ĐKXĐ: ![]()
– Quy đồng: ![]()
– Rút gọn: ![]()
b/ Tìm giá trị của ![]() để
để ![]() có giá trị nguyên:
có giá trị nguyên:
– Chia tử cho mẫu ta được: ![]() .
.
– Lý luận: ![]() nguyên
nguyên ![]() nguyên
nguyên ![]() là ước của 1 là
là ước của 1 là ![]() .
.![]()
Vậy với ![]() thì biểu thức
thì biểu thức ![]() có giá trị nguyên.
có giá trị nguyên.
Bài tập rút gọn, tính giá trị biểu thức chứa căn lớp 9:
Bài 1: Cho biểu thức ![]()
a. Rút gọn biểu thức ![]() ;
;
b. Tìm giá trị của ![]() để
để ![]() .
.
Bài 2: Cho biểu thức ![]()
a) Rút gọn biểu thức ![]() ;
;
b) Tìm giá trị của ![]() để
để ![]() .
.
Bài 3: Cho biểu thức: ![]()
a) Rút gọn biểu thức ![]() ;
;
b) Tìm giá trị của ![]() để
để ![]() .
.
Bài 4: Rút gọn biểu thức:
![]()
Bài5: Cho các biểu thức:
![]() và
và ![]()
a) Rút gọn biểu thức ![]() và
và ![]() ;
;
b) Tìm giá trị của ![]() để
để ![]() .
.
Bài 6: Cho biểu thức: ![]()
a) Rút gọn biểu thức ![]()
b) So sánh ![]() với
với ![]() .
.
c) Với mọi giá trị của ![]() làm
làm ![]() có nghĩa, chứng minh biểu thức
có nghĩa, chứng minh biểu thức ![]() chỉ nhận đúng một giá trị nguyên.
chỉ nhận đúng một giá trị nguyên.
Bài 7: Cho biểu thức:
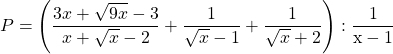
a) Tìm điều kiện để ![]() có nghĩa, rút gọn biểu thức
có nghĩa, rút gọn biểu thức ![]() ;
;
b) Tìm các số tự nhiên x để ![]() là số tự nhiên;
là số tự nhiên;
c) Tính giá trị của ![]() với
với ![]() .
.
Bài 8: Cho biểu thức : ![]()
a) Rút gọn biểu thức ![]() ;
;
b/Tìm x để ![]()
Bài 9: Cho biểu thức : ![]()
a) Rút gọn ![]()
b) Tìm a để ![]()
Bài 10: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Tìm x để ![]()
c) Tìm giá trị nhỏ nhất của ![]()
Bài 11: Cho biểu thức : ![]()
a) Rút gọn ![]()
b) Tìm giá trị của ![]() để
để ![]()
Bài 12: Cho biểu thức : ![]()
a) Rút gọn ![]()
b) Tìm các giá trị của ![]() để
để ![]()
c) Chứng minh ![]()
Bài 13: Cho biểu thức: ![]() với m > 0
với m > 0
a) Rút gọn ![]()
b) Tính ![]() theo
theo ![]() để
để ![]() .
.
c) Xác định các giá trị của ![]() để
để ![]() tìm được ở câu b thoả mãn điều kiện
tìm được ở câu b thoả mãn điều kiện ![]()
Bài 14: Cho biểu thức : ![]()
a) Rút gọn ![]()
b) Tìm ![]() để
để ![]()
c) Tìm giá trị nhỏ nhất của ![]() ?
?
Bài 15: Cho biểu thức:
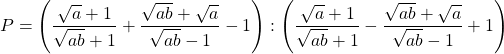
a) Rút gọn ![]()
b) Tính giá trị của ![]() nếu
nếu ![]() và
và ![]()
c) Tìm giá trị nhỏ nhất của ![]() nếu
nếu ![]()
Bài 16: Cho biểu thức:
![]()
a) Rút gọn ![]()
b) Với giá trị nào của ![]() thì
thì ![]()
c) Với giá trị nào của ![]() thì
thì ![]()
Bài 17: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Tìm các giá trị của ![]() để
để ![]()
c) Tìm các giá trị của ![]() để
để ![]()
Bài 18: Cho biểu thức: 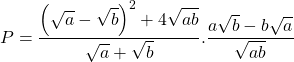
a) Tìm điều kiện để ![]() có nghĩa.
có nghĩa.
b) Rút gọn ![]()
c) Tính giá trị của ![]() khi a =
khi a =![]() và b =
và b =![]()
Bài 19: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Chứng minh rằng ![]() với
với ![]()
Bài 20: Cho biểu thức : ![]()
a) Rút gọn ![]()
b) Tính ![]() khi x =
khi x =![]()
Bài 21: Cho biểu thức: 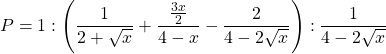
a) Rút gọn ![]()
b) Tìm giá trị của ![]() để
để ![]()
Bài 22: Cho biểu thức : 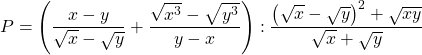
a) Rút gọn ![]()
b) Chứng minh P ![]()
Bài 23: Cho biểu thức :
![Rendered by QuickLaTeX.com \displaystyle P = \left( {\frac{1}{{\sqrt{a}+\sqrt{b}}}+\frac{{3\sqrt{{ab}}}}{{a\sqrt{a}+b\sqrt{b}}}} \right).\left[ {\left( {\frac{1}{{\sqrt{a}-\sqrt{b}}}-\frac{{3\sqrt{{ab}}}}{{a\sqrt{a}-b\sqrt{b}}}} \right):\frac{{a-b}}{{a+\sqrt{{ab}}+b}}} \right]](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-147c807aeec9e5b743b3d77e41ec970c_l3.png)
a) Rút gọn ![]()
b) Tính P khi ![]() và
và ![]()
Bài 24: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Cho ![]() tìm giá trị của a
tìm giá trị của a
c) Chứng minh rằng ![]()
Bài 25: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Với giá trị nào của ![]() thì
thì ![]()
Bài 26: Cho biểu thức:
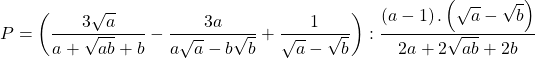
a) Rút gọn ![]()
b) Tìm những giá trị nguyên của ![]() để
để ![]() có giá trị nguyên
có giá trị nguyên
Bài 27: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Tìm giá trị của ![]() để
để ![]()
Bài 28: Cho biểu thức:
![Rendered by QuickLaTeX.com \displaystyle P=\left[ {\left( {\frac{1}{{\sqrt{x}}}+\frac{1}{{\sqrt{y}}}} \right).\frac{2}{{\sqrt{x}+\sqrt{y}}}+\frac{1}{x}+\frac{1}{y}} \right]:\frac{{\sqrt{{{{x}^{3}}}}+y\sqrt{x}+x\sqrt{y}+\sqrt{{{{y}^{3}}}}}}{{\sqrt{{{{x}^{3}}y}}+\sqrt{{x{{y}^{3}}}}}}](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-6bf7145594dd3ffd76d1dfd97b3177f2_l3.png)
a) Rút gọn ![]()
b) Cho ![]() . Xác định
. Xác định ![]() để P có giá trị nhỏ nhất
để P có giá trị nhỏ nhất
Bài 29: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) Tìm tất cả các số nguyên dương x để y=625 và P<0,2
Bài 30: Cho biểu thức: ![]()
a) Rút gọn ![]()
b) So sánh ![]() với
với ![]()
