Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
- Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
- Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau khi rút gọn
- Đồ thị hàm số bậc nhất và bậc hai
- Giải và biện luận phương trình bậc nhất một ẩn
- Giải và biện luận hệ phương trình bậc nhất hai ẩn
- Phương trình bậc hai – Hệ thức Vi-ét
- Cách tìm hai số khi biết tổng và tích của chúng
- Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
- Hệ phương trình bậc nhất chứa tham số
- Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
- Biện luận nghiệm của phương trình bậc 2 bằng đồ thị
- Các dạng bài tập giải bài toán bằng cách lập phương trình, hệ phương trình
- 30 bài tập hình học ôn thi vào 10 môn Toán
- Dạng bài tìm điều kiện về nghiệm của phương trình bậc hai
- Bài tập: Rút gọn biểu thức và câu hỏi phụ – Ôn thi vào 10
- Bài tập bất đẳng thức lớp 9 không chuyên
- 32 bài tập giải bài toán bằng cách lập phương trình, hệ phương trình cơ bản
- Các dạng bài tập Đại số ôn thi vào lớp 10
- Ôn thi vào 10 môn Toán năm học 2020-2021
- 5 đề thi thử vào lớp 10 THPT môn Toán năm 2021
- Đề thi thử môn Toán vào lớp 10 THPT năm 2021-2022 có lời giải
- Chuyên đề: Phương trình và hệ phương trình ôn thi vào 10
- 68 bài tập: giải toán bằng cách lập phương trình, hệ phương trình
- Một số bài hình ôn thi vào lớp 10 có lời giải
- Những bài toán hình học mẫu ôn thi HK2 và tuyển sinh vào 10 môn Toán
Cách nhận biết, phương pháp giải hệ phương trình đối xứng loại 1, loại 2 có hai ẩn x, y qua các ví dụ và bài tập có lời giải.
Dựa vào lý thuyết đa thức đối xứng ta định nghĩa về PT đối xứng như sau:
Phương trình
ẩn
gọi là đối xứng với ẩn nếu thay bởi bởi
thì phương trình không thay đổi.
– Khi đó phương trình luôn được biểu diễn dưới dạng:
![]()
![]()
………………………….
![]()
I. Hệ phương trình đối xứng loại 1
– Hệ phương trình đối xứng loại một là hệ mà trong đó gồm các phương trình đối xứng.
– Để giải được hệ phương trình đối xứng loại 1 ta phải dùng định lý Viét.
* Nếu đa thức ![]() có nghiệm trên
có nghiệm trên ![]() là
là ![]() thì:
thì:
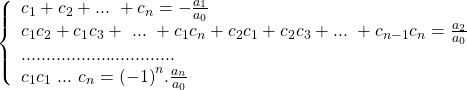
(Định lý Viét tổng quát)
1. Định lý Viét cho phương trình bậc 2
Nếu phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm x1, x2 thì:
![]()
Ngược lại, nếu 2 số x1, x2 có ![]() thì
thì ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]()
2. Định nghĩa
Hệ phương trình đối xứng loại 1 hai ẩn có dạng:
![]() , trong đó
, trong đó ![]() .
.
3. Cách giải hệ phương trình đối xứng loại 1 có 2 ẩn
Bước 1: Đặt điều kiện (nếu có).
Bước 2: Đặt S = x + y, P = xy với điều kiện của S, P và ![]() .
.
Bước 3: Thay ![]() bởi
bởi ![]() vào hệ phương trình. Giải hệ tìm
vào hệ phương trình. Giải hệ tìm ![]() rồi dùng Viét đảo tìm
rồi dùng Viét đảo tìm ![]() .
.
Chú ý:
+ Cần nhớ: ![]()
+ Đôi khi ta phải đặt ẩn phụ ![]() và
và ![]()
+ Có những hệ phương trình trở thành đối xứng loại 1 sau khi đặt ẩn phụ.
4. Bài tập giải hệ PT đối xứng loại 1
– Loại 1: Giải hệ phương trình
Ví dụ 1. Giải hệ phương trình ![]() .
.
GIẢI
Đặt ![]() , điều kiện
, điều kiện ![]() . Hệ phương trình trở thành:
. Hệ phương trình trở thành:
![]()
![]()
Ví dụ 2. Giải hệ phương trình ![]() .
.
GIẢI
Đặt ![]() , điều kiện
, điều kiện ![]() . Hệ phương trình trở thành:
. Hệ phương trình trở thành:
![]()
![]()
Ví dụ 3. Giải hệ phương trình 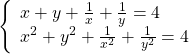 .
.
GIẢI
Điều kiện ![]() .
.
Hệ phương trình tương đương với: 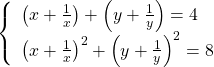
Đặt ![]() ta có:
ta có:
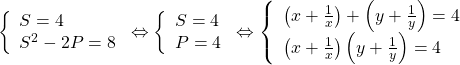
![]()
Ví dụ 4. Giải hệ phương trình ![]() .
.
GIẢI
Điều kiện ![]() . Đặt
. Đặt ![]() , ta có:
, ta có:
![]() và
và ![]() .
.
Thế vào (1), ta được: ![]()
Suy ra: ![]()
– Loại 2: Điều kiện tham số để hệ đối xứng loại (kiểu) 1 có nghiệm
Phương pháp giải chung:
+ Bước 1: Đặt điều kiện (nếu có).
+ Bước 2: Đặt ![]() với điều kiện của
với điều kiện của ![]() và (*)
và (*)
+ Bước 3: Thay ![]() bởi
bởi ![]() vào hệ phương trình.
vào hệ phương trình.
Giải hệ tìm ![]() theo
theo ![]() rồi từ điều kiện (*) tìm
rồi từ điều kiện (*) tìm ![]() .
.
Chú ý:
Khi ta đặt ẩn phụ ![]() và
và ![]() thì nhớ tìm chính xác điều kiện của
thì nhớ tìm chính xác điều kiện của ![]() .
.
Ví dụ 1 (trích đề thi ĐH khối D – 2004). Tìm điều kiện m để hệ phương trình sau có nghiệm thực:
![]()
GIẢI
Điều kiện ![]() ta có:
ta có:
![]()
Đặt ![]() ,
, ![]() Hệ phương trình trở thành:
Hệ phương trình trở thành:
![]() .
.
Từ điều kiện ![]() ta có
ta có ![]() .
.
Ví dụ 2. Tìm điều kiện ![]() để hệ phương trình
để hệ phương trình ![]() có nghiệm thực.
có nghiệm thực.
Giải
![]() .
.
Đặt ![]() Hệ phương trình trở thành:
Hệ phương trình trở thành: ![]() .
.
Suy ra ![]() và
và ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
![]()
Từ điều kiện ta suy ra hệ có nghiệm ![]() .
.
Loại 3: Một số bài toán giải bằng cách đưa về hệ phương trình.
Ví dụ. Giải phương trình: ![]() .
.
Giải
Đặt: ![]() . Vậy ta có hệ:
. Vậy ta có hệ: ![]()
⇔ ![Rendered by QuickLaTeX.com \displaystyle \left\{ \begin{array}{l}u+v=\frac{3}{2}\\(u+v)\left[ {{(u+v)}^{2}}-3uv \right]=1\end{array} \right.](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-744a18f6e72a1bd49a421b19dae6226a_l3.png)
⇔ ![]()
u, v là hai nghiệm của phương trình: ![]()
⇒ 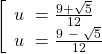 ⇒
⇒ 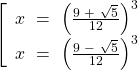
Vậy phương trình có hai nghiệm: ![]() =
= 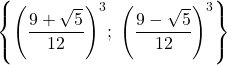 .
.
II. Hệ phương trình đối xứng loại 2 có 2 ẩn
A. Định nghĩa
Hệ phương trình đối xứng loại 2 hai ẩn có dạng:
B. Cách giải hệ PT đối xứng loại 2 có 2 ẩn
Lấy (1) – (2) hoặc (2) – (1) ta được: ![]() .
.
Khi đó ![]() hoặc
hoặc ![]()
+ Trường hợp 1: ![]() kết hợp với phương trình hoặc suy ra được nghiệm.
kết hợp với phương trình hoặc suy ra được nghiệm.
+ Trường hợp 2: ![]() kết hợp với phương trình suy ra nghiệm (trong trường hợp này hệ phương trình mới trở về hệ đối xứng loại 1) và thông thường vô nghiệm.
kết hợp với phương trình suy ra nghiệm (trong trường hợp này hệ phương trình mới trở về hệ đối xứng loại 1) và thông thường vô nghiệm.
C. Ví dụ giải hệ PT đối xứng loại 2 có lời giải
Ví dụ 1: Giải hệ phương trình ![]() (I)
(I)
GIẢI
Lấy (1) – (2) ta được: ![]()
Trường hợp 1: (I) ![]()
⇔ 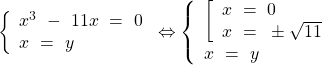 .
.
Trường hợp 2: (I) ![]() (hệ này vô nghiệm)
(hệ này vô nghiệm)
Vậy hệ phương trình đã cho có tập nghiệm:
![]()
Ví dụ 2: Giải hệ phương trình ![]()
Giải
Đặt: ![]()
Hệ phương trình trở thành:
![]()
⇔ ![]()
(Do u, v ≥ 0) ![]() .
.
Vậy hệ có nghiệm (1,1)
Đại số 9 - Tags: hệ phương trình, hệ PT đối xứng, hệ PT đối xứng loại 1, hệ PT đối xứng loại 2, toán 9Cách tìm hai số khi biết tổng và tích của chúng
Phương trình bậc hai – Hệ thức Vi-ét
Giải và biện luận hệ phương trình bậc nhất hai ẩn
Giải và biện luận phương trình bậc nhất một ẩn
Đồ thị hàm số bậc nhất và bậc hai
Cách giải phương trình bậc cao – Bồi dưỡng Toán 9
Giải phương trình vô tỷ bằng phương pháp nâng lên lũy thừa
