Phương pháp giải hệ phương trình bậc cao
- 268 bài tập nâng cao Đại số 9 có lời giải
- Cách giải phương trình bậc cao – Bồi dưỡng Toán 9
- 17 chuyên đề bồi dưỡng học sinh giỏi Toán 9 – Đặng Thành Nam
- 270 bài tập Đại số bồi dưỡng HSG lớp 9 có hướng dẫn giải
- Bồi dưỡng học sinh giỏi toán Đại số 9
- Bồi dưỡng học sinh giỏi toán Hình học 9
- Sách Tài liệu chuyên toán Đại số 9
- Sách Tài liệu chuyên toán Hình Học 9
- Phương pháp giải hệ phương trình bậc cao
- Chuyên đề: Tam giác đồng dạng – Toán nâng cao lớp 9
- Bài tập Hình học 9 chương 2 chọn lọc
- Bài tập nâng cao: Hệ thức lượng trong tam giác vuông, tỷ số lượng giác góc nhọn
- Bài tập nâng cao: Sự xác định đường tròn, quan hệ hai đường tròn, góc với đường tròn
- Cách chứng minh đường thẳng đi qua điểm cố định
Giải hệ phương trình bậc cao là dạng bài tập khó thường xuất hiện ở trong đề thi HSG Toán lớp 9, đề thi môn vào 10 chuyên Toán.
Muốn giải được các hệ phương trình bậc cao các em học sinh đọc những phương pháp dưới đây.
Phương pháp đưa về hằng đẳng thức
Đây là phương pháp mà chúng ta nên chú ý đầu tiên. Chúng ta cần để ý xem phương trình trong hệ có thể biến đổi về các hằng đẳng thức đã học hay không.
Chúng ta xét các ví dụ dưới đây để hiểu về phương pháp này.
Ví dụ 1: Giải các hệ phương trình sau
a) ![]()
b) ![]()
Giải
a) Điều kiện: ![]() . Phương trình (1) tương đương:
. Phương trình (1) tương đương:
![]()
Đặt ![]() . Ta có phương trình:
. Ta có phương trình: ![]() ⇔
⇔ ![]() . Do
. Do ![]() suy ra phương trình cho ta
suy ra phương trình cho ta ![]()
![]() thay vào ta có:
thay vào ta có: ![]() Đặt
Đặt ![]() ta có hệ phương trình sau:
ta có hệ phương trình sau:
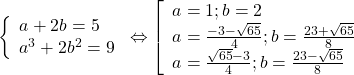 .
.
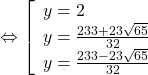
Vậy hệ có nghiệm
![]()
b) Điều kiện: ![]() .
.
Ta viết lại phương trình (1) thành: ![]()
![]()
Dễ thấy ![]() không phải là nghiệm. Khi
không phải là nghiệm. Khi ![]() thay vào (2) ta được:
thay vào (2) ta được:
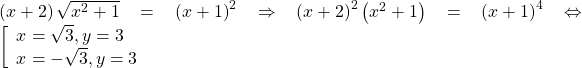
(thỏa mãn). Vậy hệ có nghiệm ![]() .
.
Ví dụ 2: Giải các hệ phương trình sau
a) ![]()
b) ![]()
Giải
a) Điều kiện: ![]() .
.
Ta thấy ![]() không là nghiệm của hệ. chia hai vế của (1) cho
không là nghiệm của hệ. chia hai vế của (1) cho ![]() ta được:
ta được:
![]() . Đặt
. Đặt ![]() ta có phương trình:
ta có phương trình: ![]() suy ra
suy ra ![]()
![]() . Từ đó tính được
. Từ đó tính được ![]()
Vậy hệ đã cho có nghiệm ![]() .
.
b) Điều kiện: ![]() .Ta thấy khi thì hệ không có nghiệm.
.Ta thấy khi thì hệ không có nghiệm.
Chia phương trình (1) cho ![]() :
:
![]()
![]()
Đặt ![]() . Ta có
. Ta có ![]() ⇒
⇒ ![]() ⇔
⇔ ![]() .
.
Thay vào (2) ta được: ![]() .
.
⇔ ![]() . Vậy hệ có nghiệm
. Vậy hệ có nghiệm ![]() .
.
Áp dụng công thức nghiệm Δ của phương trình bậc 2
Khi trong hệ phương trình có chứa phương trình bậc 2 theo ẩn x, hoặc y ta biến đổi x theo y hoặc y theo x dựa vào công thức nghiệm Δ của phương trình bậc 2. Cụ thể như sau:
* Nếu Δ chẵn, ta giải x theo y rồi thế vào phương trình còn lại của hệ để giải tiếp
* Nếu Δ không chẵn ta thường xử lý theo cách:
+ Cộng hoặc trừ các phương trình của hệ để tạo được phương trình bậc hai có chẵn hoặc tạo thành các hằng đẳng thức
+ Dùng điều kiện Δ ≥ 0 để tìm miền giá trị của biến x, y. Sau đó đánh giá phương trình còn lại trên miền giá trị x, y vừa tìm được:
Minh họa cách làm này qua những ví dụ dưới đây.
Ví dụ 3: Giải các hệ phương trình sau
a) ![]()
b) ![]()
Giải
Xét phương trình (1) của hệ ta có:
![]() . Ta coi đây là phương trình bậc 2 của
. Ta coi đây là phương trình bậc 2 của ![]() thì ta có:
thì ta có: ![]() . Từ đó suy ra
. Từ đó suy ra
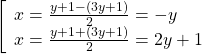
Trường hợp 1: ![]() . Từ phương trình của hệ ta có điều kiện:
. Từ phương trình của hệ ta có điều kiện: ![]() suy ra phương trình vô nghiệm
suy ra phương trình vô nghiệm
Trường hợp 2: ![]() thay vào phương trình thứ hai ta có:
thay vào phương trình thứ hai ta có:
![]()
Vậy hệ có một cặp nghiệm: ![]()
b) Xét phương trình (1) của hệ ta có:
![]()
Coi đây là phương trình bậc 2 của ![]() ta có:
ta có:
![]()
Suy ra 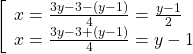
Trường hợp 1: ![]() thay vào phương trình (2) ta thu được:
thay vào phương trình (2) ta thu được:
![]()
⇔ ![]()
Do ![]() nên
nên ![]()
⇒ ![]()
Trường hợp 2: ![]() thay vào phương trình (2) ta thu được:
thay vào phương trình (2) ta thu được:
![]()
Giải tương tự như trên ta được ![]() .
.
Kết luận: Hệ phương trình có 2 cặp nghiệm: ![]()
Phương pháp đánh giá
Để giải được hệ phương trình bằng phương pháp đánh giá ta cần nắm chắc các bất đẳng thức cơ bản như: Cauchy, Bunhicopxki, các phép biến đổi trung gian giữa các bất đẳng thức, qua đó để đánh giá tìm ra quan hệ ![]() .
.
Ngoài ra ta cũng có thể dùng hàm số để tìm GTLN, GTNN từ đó có hướng đánh giá, so sánh phù hợp.
Ví dụ 4: Giải các hệ phương trình sau
a) 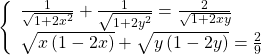
b) ![Rendered by QuickLaTeX.com \left\{ \begin{array}{l}x\left( {{x}^{2}}-{{y}^{2}} \right)+{{x}^{2}}=2\sqrt{{{\left( x-{{y}^{2}} \right)}^{3}}}\\76{{x}^{2}}-20{{y}^{2}}+2=\sqrt[3]{4x\left( 8x+1 \right)}\end{array} \right.](https://abcdonline.vn/wp-content/ql-cache/quicklatex.com-5083a6523eca11e1e52c95329c81e80e_l3.png)
Giải
a) Điều kiện: ![]() .
.
Đặt ![]() .
.
Ta có: ![]() .
.
Ta sử dụng bổ đề với ![]() và
và ![]() ta có bất đẳng thức:
ta có bất đẳng thức:
![]() (đúng).
(đúng).
Vậy ![]() .
.
Đẳng thức xảy ra khi ![]() . Thay vào(2) ta tìm được nghiệm của phương trình.
. Thay vào(2) ta tìm được nghiệm của phương trình.
Nghiệm của hệ ![]() .
.
b) Điều kiện: ![]() .
.
Phương trình (1) tương đương: ![]() .
.
Đặt ![]() phương trình (1) thành:
phương trình (1) thành:
![]()
Thay vào (2) ta được: ![]() .
.
Ta có ![]()
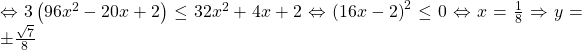
Từ đó ta có các nghiệm của hệ là: Vậy hệ có nghiệm ![]() .
.
Bài tập giải hệ PT bậc cao
Bài 1: Giải hệ phương trình ![]()
Bài 2: Giải hệ phương trình ![]()
Bài 3: Giải hệ phương trình ![]()
Bài 4: Giải hệ phương trình: ![]()
Bài 5: Tìm ![]() thỏa mãn :
thỏa mãn : ![]()
Cách tìm hệ số a, b của hàm số bậc nhất y = ax + b
270 bài tập Đại số bồi dưỡng HSG lớp 9 có hướng dẫn giải
268 bài tập nâng cao Đại số 9 có lời giải
Đề kiểm tra 45 phút Đại số 9 chương I trường THCS Giảng Võ
Đề cương ôn tập chương 1 – Đại số 9
Chuyên đề: Giải bài toán bằng cách lập hệ phương trình lớp 9
39 câu trắc nghiệm rút gọn biểu thức có đáp án – Đại số 9
