5 đề thi thử vào lớp 10 THPT môn Toán năm 2021

Đây là bài thứ 20 of 25 trong chuyên đề Ôn thi vào lớp 10 môn Toán

5 đề thi thử tuyển sinh vào lớp 10 THPT môn Toán năm học 2021-2022 được Gia sư Tiến Bộ sưu tầm chia sẻ tới các em học sinh.

Đây là các đề thi cơ bản, các em cần chăm chỉ ôn luyện làm đề, quen với các dạng bài. Từ đó nâng cao kiến thức môn Toán, chuẩn bị tốt cho môn thi Toán trong kì thi vào lớp 10.

ĐỀ SỐ 1

Câu 1) Cho biểu thức:

$\displaystyle A=\left( {\frac{2}{{\sqrt{x}-2}}+\frac{3}{{2\sqrt{x}+1}}-\frac{{5\sqrt{x}-7}}{{2x-3\sqrt{x}-2}}} \right):\frac{{2\sqrt{x}+3}}{{5x-10\sqrt{x}}}$

$\displaystyle \left( {x>0,x\ne 4} \right)$

1) Rút gọn biểu thức $\displaystyle A$

2) Tính giá trị của $\displaystyle A$

khi $\displaystyle x=3-2\sqrt{2}$

3) Tìm $\displaystyle x$ sao cho $\displaystyle A$

nhận giá trị là một số nguyên.

Câu 2) Cho phương trình $\displaystyle {{x}^{2}}-\left( {m-1} \right)-{{m}^{2}}+m-2=0$ , với $\displaystyle m$ là tham số.
a) Chứng minh rằng phương trình đã cho có hai nghiệm trái dấu với mọi $\displaystyle m$ .

b) Gọi hai nghiệm của phương trình đã cho là $\displaystyle {{x}_{1}},{{x}_{2}}$ . Tìm $\displaystyle m$ để biểu thức $\displaystyle A={{\left( {\frac{{{{x}_{1}}}}{{{{x}_{2}}}}} \right)}^{3}}-{{\left( {\frac{{{{x}_{2}}}}{{{{x}_{1}}}}} \right)}^{3}}$ đạt giá trị lớn nhất.

Câu 3) Một ca nô xuôi dòng 78km và ngược dòng 44 km mất 5 giờ với vận tốc dự định. nếu ca nô xuôi 13 km và ngược dòng 11 km với cùng vận tốc dự định đó thì mất 1 giờ. Tính vận tốc riêng của ca nô và vận tốc dòng nước.

Câu 4) Từ điểm $\displaystyle K$ nằm ngoài đường tròn $\displaystyle \left( O \right)$ ta kẻ các tiếp tuyến $\displaystyle KA,KB$ cát tuyến $\displaystyle KCD$ đến $\displaystyle \left( O \right)$ sao cho tia $\displaystyle KC$ nằm giữa hai tia $\displaystyle KA,KO$ . Gọi $\displaystyle H$ là trung điểm $\displaystyle CD$ .

a) Chứng minh: 5 điểm $\displaystyle A,K,B,O,H$ cùng nằm trên một đường tròn.

b) Gọi $\displaystyle M$ là trung điểm của $\displaystyle AB$ . Chứng minh: Tứ giác $\displaystyle MODC$ nội tiếp.

c) Đường thẳng qua $\displaystyle H$ song song với $\displaystyle BD$ cắt $\displaystyle AB$ tại $\displaystyle I$ . Chứng minh $\displaystyle CI\bot OB$ .

Câu 5) Cho các số thực $\displaystyle x,y,z$ thỏa mãn điều kiện: $\displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=2$ . Chứng minh rằng: $\displaystyle x+y+z\le xyz+2$ .

ĐỀ SỐ 2

Câu 1) Cho biểu thức:

$\displaystyle P=\left( {\frac{{2\left( {a+b} \right)}}{{\sqrt{{{{a}^{3}}-2\sqrt{{2{{b}^{3}}}}}}}}-\frac{{\sqrt{a}}}{{a+\sqrt{{2ab}}+2b}}} \right).\left( {\frac{{\sqrt{{{{a}^{3}}}}+2\sqrt{{2{{b}^{3}}}}}}{{2b+\sqrt{{2ab}}}}-\sqrt{a}} \right)$ .

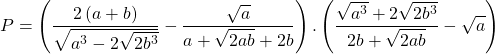a) Tìm điều kiện của $\displaystyle \displaystyle a$ và $\displaystyle b$ để biểu thức $\displaystyle P$ xác định. Rút gọn biểu thức $\displaystyle P$ .
b) Biết $\displaystyle a=1+\frac{{\sqrt{3}}}{2}$ và $\displaystyle b=\frac{1}{2}-\frac{{\sqrt{3}}}{4}$ . Tính giá trị của $\displaystyle P$ .

Câu 2) Cho phương trình $\displaystyle 2{{x}^{2}}+2mx+{{m}^{2}}-2=0$ , với $\displaystyle m$ là tham số. Gọi $\displaystyle {{x}_{1}},{{x}_{2}}$ là hai nghiệm của phương trình.

a) Tìm hệ thức liên hệ giữa $\displaystyle {{x}_{1}},{{x}_{2}}$ không phụ thuộc vào $\displaystyle m$ .

b) Tìm giá trị nhỏ nhất và lớn nhất của biểu thức $\displaystyle A=\frac{{2{{x}_{1}}{{x}_{2}}+3}}{{x_{1}^{2}+x_{2}^{2}+2\left( {{{x}_{1}}{{x}_{2}}+1} \right)}}$ .

Câu 3) Hưởng ứng phong trào “Vì biển đảo Trường Sa” một đôi tàu dự định chở 280 tấn hàng ra đảo. Nhưng khi chuẩn bị khởi hành thì số hàng hóa đã tăng thêm 6 tấn so với dự định. vì vậy đội tàu phải bổ sung thêm 1 tàu và mỗi tàu chở ít hơn dự định 2 tấn hàng. Hỏi khi dự định đội tàu có bao nhiêu chiếc tàu, biết các tàu chở số tấn hàng bằng nhau.

Câu 4) Cho hệ phương trình: $\displaystyle \left\{ \begin{array}{l}x+my=m+1\\mx+y=3m-1\end{array} \right.$

Tìm $\displaystyle m$ để hệ trên có nghiệm duy nhất sao cho $\displaystyle x.y$ đạt giá trị nhỏ nhất.

Câu 5) Cho nửa đường tròn $\displaystyle \left( {O;R} \right)$ đường kính $\displaystyle BC$ . $\displaystyle A$

là một điểm di động trên nửa đường tròn. Vẽ $\displaystyle AH$ vuông góc với $\displaystyle BC$ tại $\displaystyle H$ . Đường tròn đường kính $\displaystyle AH$ cắt $\displaystyle AB,AC$ và nửa đường tròn $\displaystyle \left( O \right)$ lần lượt tại $\displaystyle D,E,M$ . $\displaystyle AM$ cắt $\displaystyle BC$ tại $\displaystyle N$ .

a) Chứng minh rằng tứ giác $\displaystyle ADHE$ là hình chữ nhật và $\displaystyle \widehat{{AME}}=\widehat{{ACN}}$ .

b) Tính $\displaystyle \frac{{D{{E}^{3}}}}{{BD.CE}}$ theo $\displaystyle \displaystyle R$ và chứng minh rằng $\displaystyle D,E,N$ thẳng hàng.

c) Xác định vị trí điểm $\displaystyle A$

để diện tích tam giác $\displaystyle \displaystyle ABH$ lớn nhất.

Câu 6) Cho $\displaystyle x,y>0$ và $\displaystyle {{x}^{2}}+{{y}^{3}}\ge {{x}^{3}}+{{y}^{4}}$ . Chứng minh rằng: $\displaystyle {{x}^{3}}+{{y}^{3}}\le 2$ .

ĐỀ SỐ 3

Câu 1) Cho $\displaystyle b>a>0$ . Xét biểu thức: $\displaystyle P=\frac{{\sqrt{{{{a}^{3}}}}-\sqrt{{{{b}^{3}}}}}}{{a-b}}-\frac{a}{{\sqrt{a}+\sqrt{b}}}-\frac{b}{{\sqrt{b}-\sqrt{a}}}$ .
a) Rút gọn $\displaystyle P$ .

b) Biết $\displaystyle \left( {a-1} \right)\left( {b-1} \right)+2\sqrt{{ab}}=1$ , hãy tính giá trị của biểu thức $\displaystyle P$ .

Câu 2) Cho Parabol $\displaystyle (P):y={{x}^{2}}$ và đường thẳng $\displaystyle (d):y=mx+4$ .

a) Chứng minh đường thẳng $\displaystyle (d)$ luôn cắt đồ thị $\displaystyle (P)$ tại hai điểm phân biệt $\displaystyle A,B$ .Gọi $\displaystyle {{x}_{1}},{{x}_{2}}$ là hoành độ của các điểm $\displaystyle A,B$ .

Tìm giá trị lớn nhất của $\displaystyle Q=\frac{{2\left( {{{x}_{1}}+{{x}_{2}}} \right)+7}}{{{{x}_{1}}^{2}+{{x}_{2}}^{2}}}$ .

b) Tìm $\displaystyle m$ để diện tích tam giác $\displaystyle OAB$ bằng $\displaystyle 8$ .

Câu 3) Một ô tô và một xe máy khởi hành cùng một lúc từ hai tỉnh $\displaystyle A,B$ cách nhau 150km, đi ngược chiều và gặp nhau sau $\displaystyle 1,5$ h. Hỏi sau khi gặp nhau bao lâu thì ô tô đến $\displaystyle B$ và xe máy đến $\displaystyle A$

biết rằng vận tốc của xe máy bằng $\displaystyle \frac{2}{3}$ vận tốc của ô tô.

Câu 4) Cho tam giác $\displaystyle ABC$ vuông tại $\displaystyle A$

và $\displaystyle AB<AC$ . Gọi $\displaystyle H$ là hình chiếu của $\displaystyle A$

trên $\displaystyle BC$ và $\displaystyle M$ là một điểm đối xứng của $\displaystyle H$ qua $\displaystyle AB$ . Tia $\displaystyle MC$ cắt đường tròn ngoại tiếp tam giác $\displaystyle ABH$ tại điểm $\displaystyle P\left( {P\ne M} \right)$ . Tia $\displaystyle HP$ cắt đường tròn ngoại tiếp tam giác $\displaystyle APC$ tại điểm $\displaystyle N\left( {N\ne P} \right)$ .

a) Chứng minh rằng $\displaystyle HN=MC$ .

b) Gọi $\displaystyle E$ là giao điểm thứ hai của $\displaystyle AB$ với đường tròn ngoại tiếp tam giác $\displaystyle APC$ .

Chứng minh rằng $\displaystyle EN$ song song với $\displaystyle BC$ .

c) Gọi $\displaystyle K$ là giao điểm thứ hai của $\displaystyle BC$ với đường tròn ngoại tiếp tam giác $\displaystyle APC$ .

Chứng minh rằng $\displaystyle H$ là trung điểm $\displaystyle BK$ .

Câu 5) Cho các số $\displaystyle a,b,c$ không âm. Chứng minh rằng:

$\displaystyle {{a}^{3}}+{{b}^{3}}+{{c}^{3}}\ge {{a}^{2}}\sqrt{{bc}}+{{b}^{2}}\sqrt{{ca}}+{{c}^{2}}\sqrt{{ab}}$ .

ĐỀ SỐ 4

Câu 1) Cho biểu thức 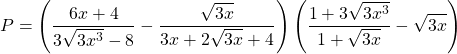$\displaystyle P=\left( {\frac{{6x+4}}{{3\sqrt{{3{{x}^{3}}}}-8}}-\frac{{\sqrt{{3x}}}}{{3x+2\sqrt{{3x}}+4}}} \right)\left( {\frac{{1+3\sqrt{{3{{x}^{3}}}}}}{{1+\sqrt{{3x}}}}-\sqrt{{3x}}} \right)$ .

a) Rút gọn $\displaystyle P$ .

b) Xác định $\displaystyle x$ nguyên sao cho $\displaystyle P$ nguyên.

Câu 2) Trong mặt phẳng tọa độ $\displaystyle Oxy$ , cho parabol $\displaystyle \left( P \right)$ có phương trình $\displaystyle y=\frac{{-{{x}^{2}}}}{2}$ . Gọi $\displaystyle \left( d \right)$ là đường thẳng đi qua $\displaystyle I\left( {0;-2} \right)$ và có hệ số góc $\displaystyle k$ .

a) Viết phương trình đường thẳng $\displaystyle \left( d \right)$ . Chứng minh đường thẳng $\displaystyle \left( d \right)$ luôn cắt parabol $\displaystyle \left( P \right)$ tại hai điểm phân biệt $\displaystyle A,B$ khi $\displaystyle k$ thay đổi.

b) Gọi $\displaystyle H,K$ theo thứ tự là hình chiếu vuông góc của $\displaystyle A,B$ trên trục hoành. Chứng minh rằng tam giác $\displaystyle IHK$ vuông tại $\displaystyle I$ .

Câu 3) Giải hệ phương trình 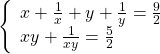$\displaystyle \left\{ \begin{array}{l}x+\frac{1}{x}+y+\frac{1}{y}=\frac{9}{2}\\xy+\frac{1}{{xy}}=\frac{5}{2}\end{array} \right.$ .

Câu 4) Cho đường tròn $\displaystyle \left( O \right)$ và điểm $\displaystyle A$

nằm ngoài đường tròn $\displaystyle \left( O \right)$ . Từ $\displaystyle A$

vẽ hai tiếp tuyến $\displaystyle AB,AC$ của đường tròn $\displaystyle \left( O \right)$ ( $\displaystyle B,C$ là hai tiếp điểm). Gọi $\displaystyle H$ là giao điểm của $\displaystyle AO$ và $\displaystyle BC.$ Qua $\displaystyle A$

vẽ cát tuyến $\displaystyle \displaystyle ADE$ của đường tròn $\displaystyle \left( {IO} \right)$ ; $\displaystyle D$ và $\displaystyle E$ thuộc đường tròn $\displaystyle \left( O \right)$ sao cho đường thẳng $\displaystyle AE$ cắt đoạn thẳng $\displaystyle HB$ tại $\displaystyle I$ . Gọi $\displaystyle M$ là trung điểm dây cung $\displaystyle DE$ .

a) Chứng minh $\displaystyle A{{B}^{2}}=AD.AE$ .

b) Chứng minh năm điểm $\displaystyle A,B,M,O,C$ cùng thuộc một đường tròn.

c) Chứng minh tứ giác $\displaystyle OHDE$ nội tiếp.

d) Trên tia đối của tia $\displaystyle HD$ lấy điểm $\displaystyle F$ sao cho $\displaystyle H$ là trung điểm $\displaystyle DF$ . Tia $\displaystyle AO$ cắt đường thẳng $\displaystyle EF$ tại $\displaystyle K$ . Chứng minh $\displaystyle IK//DF$ .

Câu 5) Cho $\displaystyle a,b,c\in \left[ {\frac{1}{2};1} \right]$ . Chứng minh rằng: $\displaystyle 2\le \frac{{a+b}}{{1+c}}+\frac{{b+c}}{{1+a}}+\frac{{c+a}}{{1+b}}\le 3$ .

ĐỀ SỐ 5

Câu 1) Cho $\displaystyle P=\left( {\frac{{\sqrt{x}+3}}{{\sqrt{x}-2}}+\frac{{\sqrt{x}+2}}{{3-\sqrt{x}}}+\frac{{\sqrt{x}+2}}{{x-5\sqrt{x}+6}}} \right):\left( {1-\frac{{\sqrt{x}}}{{\sqrt{x}+1}}} \right)$

a) Rút gọn $\displaystyle P$ .

b) Tìm $\displaystyle x$ nguyên để $\displaystyle P<0$ .

c) Tìm $\displaystyle x$ để $\displaystyle Q=\frac{1}{P}$ nhỏ nhất.

Câu 2) Cho parabol $\displaystyle \left( P \right):y={{x}^{2}}$ và đường thẳng $\displaystyle \left( d \right):y=\left( {m+5} \right)x-m$ với $\displaystyle m$ là tham số.

a) Chứng minh rằng $\displaystyle d$ luôn cắt $\displaystyle \left( P \right)$ tại hai điểm phân biệt.

b) Gọi $\displaystyle A\left( {{{x}_{1}};{{y}_{1}}} \right),B\left( {{{x}_{2}};{{y}_{2}}} \right)$ là các giao điểm của $\displaystyle d$ và $\displaystyle \left( P \right)$ . Tìm giá trị nhỏ nhất của biểu thức $\displaystyle M=\left| {{{x}_{1}}-{{x}_{2}}} \right|$ .

Câu 3) Trên quãng đường $\displaystyle AB$ dài $\displaystyle 210$ m , tại cùng một thời điểm một xe máy khởi hành từ $\displaystyle A$

đến $\displaystyle B$ và một ôt ô khởi hành từ $\displaystyle B$ đi về $\displaystyle A$

. Sauk hi gặp nhau xe máy đi tiếp 4 giờ nữa thì đến $\displaystyle B$ và ô tô đi tiếp 2 giờ 15 phút nữa thì đến $\displaystyle A$

. Biết rằng vận tốc ô tô và xe máy không thay đổi trong suốt chặng đường. Tính vận tốc của xe máy và ô tô.

Câu 4) Cho dường tròn $\displaystyle \left( O \right)$ và dây cung $\displaystyle BC$ không là đường kính. Gọi $\displaystyle A$

là điểm chính giữa của cung lớn $\displaystyle BC$ . Các tiếp tuyến tại $\displaystyle B,C$ của $\displaystyle \left( O \right)$ cắt nhau tại $\displaystyle \displaystyle S$ . Gọi $\displaystyle H$ là hình chiếu vuông góc của $\displaystyle C$ trên $\displaystyle AB$ và $\displaystyle M$ là trung điểm của $\displaystyle CH$ . Tia $\displaystyle AM$ cắt đường tròn $\displaystyle \left( O \right)$ tại điểm thứ hai $\displaystyle N$ .

a) Gọi $\displaystyle D$ là giao điểm của $\displaystyle SA$ với $\displaystyle BC$ . Chứng minh tứ giác $\displaystyle CMDN$ nội tiếp.

b) Tia $\displaystyle SN$ cắt đường tròn $\displaystyle \left( O \right)$ tại điểm thứ hai $\displaystyle E$ . Chứng minh rằng $\displaystyle CE$ song song với $\displaystyle SA$

c) Chứng minh đường thẳng $\displaystyle CN$ đi qua trung điểm của đoạn thẳng $\displaystyle SD$ .

Câu 5) Giải hệ phương trình: $\displaystyle \left\{ \begin{array}{l}{{x}^{3}}+{{y}^{3}}+7\left( {x+y} \right)xy=8xy\sqrt{{2\left( {{{x}^{2}}+{{y}^{2}}} \right)}}\\\sqrt{y}-\sqrt{{2x-3}}=6-2x\end{array} \right.$

Cùng chuyên đề:

<< Ôn thi vào 10 môn Toán năm học 2020-2021Đề thi thử môn Toán vào lớp 10 THPT năm 2021-2022 có lời giải >>

5 đề thi thử vào lớp 10 THPT môn Toán năm 2021

5 đề thi thử tuyển sinh vào lớp 10 THPT môn Toán năm học 2021-2022 được Gia sư Tiến Bộ sưu tầm chia sẻ tới các em học sinh.

ĐỀ SỐ 1

ĐỀ SỐ 2

ĐỀ SỐ 3

ĐỀ SỐ 4

ĐỀ SỐ 5

Đề thi vào 10 môn Toán tỉnh Hà Nam 2020-2021

Đề thi vào 10 môn Toán tỉnh Thái Bình 2020-2021 có đáp án

Đề thi vào 10 môn Toán chuyên tỉnh Quảng Trị 2020-2021

Đề thi vào 10 môn Toán chuyên tỉnh Bình Phước 2020-2021

Đề thi vào 10 môn Toán chuyên Nguyễn Trãi, Hải Dương 2020-2021

Đề thi vào 10 môn Toán tỉnh Hòa Bình 2020-2021

Đề thi vào 10 THPT chuyên môn Toán tỉnh Nam Định 2020-2021