Đồ thị hàm số bậc nhất và bậc hai

Đây là bài thứ 3 of 25 trong chuyên đề Ôn thi vào lớp 10 môn Toán

Ôn thi vào lớp 10 môn Toán

Dạng toán về Đồ thị hàm số bậc nhất y=ax + b và hàm số bậc hai y=ax^2 + b rất quan trọng trong chương trình ôn thi vào 10 môn Toán.

Vì vậy các em cần học những gì mà Gia sư Tiến Bộ chia sẻ dưới đây.

I. Điểm thuộc đường – đường đi qua điểm

Điểm A(x_A; y_A) thuộc đồ thị hàm số y = f(x) ⇔ y_A = f(x_A).

Ví dụ 1: Tìm hệ số a của hàm số: y = ax² biết đồ thị hàm số của nó đi qua điểm A(2;4)

Giải:

Do đồ thị hàm số đi qua điểm A(2;4) nên: 4 = a.2² ⇔ a = 1

Ví dụ 2: Trong mặt phẳng tọa độ cho A(-2;2) và đường thẳng (d) có Phương trình:

y = -2(x + 1). Đường thẳng (d) có đi qua A không?

Giải:

Ta thấy -2.(-2 + 1) = 2 nên điểm A thuộc vào đường thẳng (d)

II. Cách tìm giao điểm của hai đường y = f(x) và y = g(x)

Bước 1: Hoành độ giao điểm là nghiệm của Phương trình f(x) = g(x) (*)

Bước 2: Lấy nghiệm đó thay vào 1 trong hai công thức y = f(x) hoặc y = g(x) để Tìm tung độ giao điểm.

Chú ý: Số nghiệm của Phương trình (*) là số giao điểm của hai đường trên.

III. Quan hệ giữa hai đường thẳng

Xét hai đường thẳng: $\left(d_{1}\right): y=a_{1} x+b_{1}$

và (d₂): $\left(d_{2}\right): y=a_{2} x+b_{2}$

a) $\left(\mathrm{d}_{1}\right)$

cắt $\left(\mathrm{d}_{2}\right) \Leftrightarrow \mathrm{a}_{1} \neq \mathrm{a}_{2}$

b) $\left.\mathrm{d}_{1}\right) / /\left(\mathrm{d}_{2}\right) \Leftrightarrow\left\{\begin{array}{l}\mathrm{a}_{1}=\mathrm{a}_{2} \\ \mathrm{b}_{1} \neq \mathrm{b}_{2}\end{array}\right.$

c) $\left.\mathrm{d}_{1}\right) \equiv\left(\mathrm{d}_{2}\right) \Leftrightarrow\left\{\begin{array}{l}\mathrm{a}_{1}=\mathrm{a}_{2} \\ \mathrm{b}_{1}=\mathrm{b}_{2}\end{array}\right.$

d) $\left(\mathrm{d}_{1}\right) \perp\left(\mathrm{d}_{2}\right) \Leftrightarrow \mathrm{a}_{1} \cdot \mathrm{a}_{2}=-1$

IV. Tìm điều kiện để 3 đường thẳng đồng quy

Bước 1: Giải hệ Phương trình gồm hai đường thẳng không chứa tham số để Tìm (x;y).

Bước 2: Thay (x;y) vừa Tìm được vào Phương trình còn lại để Tìm ra tham số.

V. Quan hệ giữa (d): y = ax + b và (P): y = ax² (a^’0)

1. Tìm tọa độ giao điểm của (d) và (P)

Bước 1: Tìm hoành độ giao điểm là nghiệm của Phương trình:

a^’x² = ax + b (#) $\displaystyle \Leftrightarrow$ a^’x²– ax – b = 0

Bước 2: Lấy nghiệm đó thay vào 1 trong hai công thức y = ax +b hoặc y = ax² để Tìm tung độ giao điểm.

Chú ý: Số nghiệm của Phương trình (#) là số giao điểm của (d) và (P).

2. Tìm điều kiện để (d) và (P) cắt; tiếp xúc; không cắt nhau

Từ Phương trình (#) ta có: $\displaystyle {{a}^{'}}{{x}^{2}}-ax-b=0\Rightarrow \Delta ={{(-a)}^{2}}+4{{a}^{'}}.b$

a) (d) và (P) cắt nhau ⇔ Phương trình (#) có hai nghiệm phân biệt $\displaystyle \Leftrightarrow \Delta >0$

b) (d) và (P) tiếp xúc với nhau ⇔ Phương trình (#) cú nghiệm kép $\displaystyle \Leftrightarrow \Delta =0$

c) (d) và (P) không giao nhau ⇔ Phương trình (#) vô nghiệm $\displaystyle \Leftrightarrow \Delta <0$

VI. Viết Phương trình đường thẳng y = ax + b

1. Biết quan hệ về hệ số góc (//hay vuông góc) và đi qua điểm A(x₀;y₀)

Bước 1: Dựa vào quan hệ song song hay vuông góc để Tìm hệ số a.

Bước 2: Thay a vừa Tìm được và x₀; y₀ vào công thức y = ax + b để Tìm b.

2. Biết đồ thị hàm số đi qua điểm A(x₁; y₁) và B(x₂; y₂).

Do đồ thị hàm số đi qua điểm A(x₁;y₁) và B(x₂;y₂) nên ta có hệ Phương trình:

Giải hệ Phương trình Tìm a,b.

3. Biết đồ thị hàm số đi qua điểm A(x₀;y₀) và tiếp xúc với (P): y = a‘x²

+) Do đường thẳng đi qua điểm A(x₀;y₀) nên có Phương trình :

y₀ = ax₀ + b

+) Do đồ thị hàm số y = ax + b tiếp xúc với (P): y = a’x² nên:

PT: a’x² = ax + b có nghiệm kép

+) Giải hệ $\displaystyle \left\{ \begin{array}{l}{{y}_{0}}=a{{x}_{0}}+b\\\Delta =0\end{array} \right.$ để Tìm a,b.

VII. Chứng minh đường thẳng luôn đi qua 1 điểm cố định

(giả sử tham số là m).

+) Giả sử A(x₀;y₀) là điểm cố định mà đường thẳng luôn đi qua với mọi m, thay x₀; y₀ vào Phương trình đường thẳng chuyển về Phương trình ẩn m hệ số x₀; y₀ nghiệm đúng với mọi m.

+) Đồng nhất hệ số của Phương trình trên với 0 giải hệ Tìm ra x₀;y₀.

VIII. Tìm khoảng cách giữa hai điểm bất kỳ A; B

Gọi x₁; x₂ lần lượt là hoành độ của A và B; y₁,y₂ lần lượt là tung độ của A và B

Đồ thị hàm số bậc nhất và bậc hai

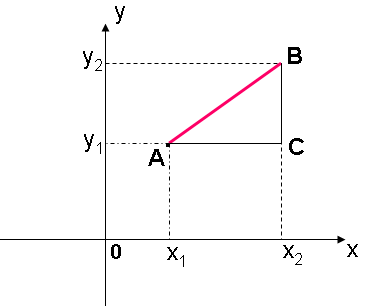
Khi đó khoảng cách AB được tính bởi định lý Pi Ta Go trong tam giác vuông ABC:

$\displaystyle AB=\sqrt{{A{{C}^{2}}+B{{C}^{2}}}}=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}$

IX. Một số ứng dụng của đồ thị hàm số

1. Ứng dụng vào Phương trình.

2. Ứng dụng vào bài toán cực trị.

BÀI TẬP VỀ HÀM SỐ

Bài 1. Cho parabol (p): y = 2x².

1. Tìm giá trị của a,b sao cho đường thẳng y = ax+b tiếp xúc với (p) và đi qua A(0;-2).

2. Tìm Phương trình đường thẳng tiếp xúc với (p) tại B(1;2).

3. Tìm giao điểm của (p) với đường thẳng y = 2m +1.

Bài 2: Cho (P) $\displaystyle y=\frac{1}{2}{{x}^{2}}$ và đường thẳng (d): y = ax + b .

1. Xác định a và b để đường thẳng (d) đi qua điểm A(-1;0) và tiếp xúc với (P).

2. Tìm toạ độ tiếp điểm.

Bài 3: Cho (P) $\displaystyle y={{x}^{2}}$ và đường thẳng (d) y = 2x + m

1. Vẽ (P)

2. Tìm m để (P) tiếp xúc (d)

3. Tìm toạ độ tiếp điểm.

Bài 4: Cho (P) $\displaystyle y=-\frac{{{{x}^{2}}}}{4}$ và (d): y = x + m

1. Vẽ (P)

2. Xác định m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B

3. Xác định Phương trình đường thẳng (d’) song song với đường thẳng (d) và cắt (P) tại điểm có tung độ bằng -4

4. Xác định Phương trình đường thẳng (d”) vuông góc với (d’) và đi qua giao điểm của (d’) và (P)

Bài 5: Cho hàm số (P): $\displaystyle y={{x}^{2}}$ và hàm số(d): y = x + m

1. Tìm m sao cho (P) và (d) cắt nhau tại hai điểm phân biệt A và B

2. Xác định Phương trình đường thẳng (d’) vuông góc với (d) và tiếp xúc với (P)

3. Tìm m sao cho khoảng cách giữa hai điểm A và B bằng $\displaystyle 3\sqrt{2}$

Bài 6: Cho điểm A(-2;2) và đường thẳng ( $\displaystyle {{d}_{1}}$ ) y = -2(x+1)

1. Điểm A có thuộc ( $\displaystyle {{d}_{1}}$ ) không ? Vì sao ?

2. Tìm a để hàm số (P): $\displaystyle y=a.{{x}^{2}}$ đi qua A

3. Xác định Phương trình đường thẳng ( $\displaystyle {{d}_{2}}$ ) đi qua A và vuông góc với ( $\displaystyle {{d}_{1}}$ )

4. Gọi A và B là giao điểm của (P) và ( $\displaystyle {{d}_{2}}$ ) ; C là giao điểm của ( $\displaystyle {{d}_{1}}$ ) với trục tung . Tìm toạ độ của B và C . Tính chu vi tam giác ABC?

Bài 7: Cho (P) $\displaystyle y=\frac{1}{4}{{x}^{2}}$ và đường thẳng (d) đi qua hai điểm A và B trên (P) có hoành độ lần lượt là

-2 và 4

1. Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số trên
2. Viết Phương trình đường thẳng (d)

3. Tìm điểm M trên cung AB của (P) tương ứng hoành độ $\displaystyle x\in \left[ {-2;4} \right]$ sao cho tam giác MAB có diện tích lớn nhất.

(Gợi ý: cung AB của (P) tương ứng hoành độ $\displaystyle x\in \left[ {-2;4} \right]$ có nghĩa là A(-2; $\displaystyle {{y}_{A}}$ ) và B(4; $\displaystyle {{y}_{B}}$ )Þ tính $\displaystyle {{y}_{{A;}}};{{y}_{B}}$ ;S_MAB có diện tích lớn nhất $\displaystyle \Leftrightarrow$ M là tiếp điểm của đường thẳng (d₁)với (P)và(d₁)//(d).

Bài 8: Cho (P): $\displaystyle y=-\frac{{{{x}^{2}}}}{4}$ và điểm M (1;-2)

1. Viết Phương trình đường thẳng (d) đi qua M và có hệ số góc là m
HD: Phương trình có dạng: $\displaystyle y=ax+b$ mà a = m. thay x = 1; y = -2 tính b = – m-2. vậy PT: $\displaystyle y=mx-m-2.$

2. Chứng minh: (d) luôn cắt (P) tại hai điểm phân biệt A và B khi m thay đổi

3. Gọi $\displaystyle {{x}_{A}};{{x}_{B}}$ lần lượt là hoành độ của A và B. Xác định m để $\displaystyle x_{A}^{2}{{x}_{B}}+{{x}_{A}}x_{B}^{2}$ đạt giá trị nhỏ nhất và tính giá trị đó?

Bài 9: Cho hàm số (P): $\displaystyle y={{x}^{2}}$

1. Vẽ (P)

2. Gọi A,B là hai điểm thuộc (P) có hoành độ lần lượt là -1 và 2. Viết phương trình đường thẳng AB

3. Viết Phương trình đường thẳng (d) song song với AB và tiếp xúc với (P)

Bài 10: Trong hệ toạ độ xOy cho Parabol (P) $\displaystyle y=-\frac{1}{4}{{x}^{2}}$ và đường thẳng (d): $\displaystyle y=mx-2m-1$

1. Vẽ (P)

2. Tìm m sao cho (P) và (d) tiếp xúc nhau.Tìm toạ độ tiếp điểm

3. Chứng tỏ rằng (d) luôn đi qua một điểm cố định

Bài 11: Cho (P): $\displaystyle y=-\frac{1}{4}{{x}^{2}}$ và điểm I(0;-2). Gọi (d) là đường thẳng qua I và có hệ số góc m.

1. Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt A và B với $\displaystyle \forall m\in R$
2.Tìm giá trị của m để đoạn AB ngắn nhất

Bài 12: Cho (P): $\displaystyle y=\frac{{{{x}^{2}}}}{4}$ và đường thẳng (d) đi qua điểm I( $\displaystyle \frac{3}{2};1$ ) có hệ số góc là m

1. Vẽ (P) và viết Phương trình (d)

2. Tìm m sao cho (d) tiếp xúc (P)

3. Tìm m sao cho (d) và (P) có hai điểm chung phân biệt

Bài 13: Cho (P): $\displaystyle y=\frac{{{{x}^{2}}}}{4}$ và đường thẳng (d): $\displaystyle y=-\frac{x}{2}+2$

1. Vẽ (P) và (d)

2. Tìm toạ độ giao điểm của (P) và (d)

3. Tìm toạ độ của điểm thuộc (P) sao cho tại đó đường tiếp tuyến của (P) song song với (d)

Bài 14: Cho (P): $\displaystyle y={{x}^{2}}$

1. Gọi A và B là hai điểm thuộc (P) có hoành độ lần lượt là -1 và 2. Viết phương trình đường thẳng AB

2. Viết Phương trình đường thẳng (d) song song với AB và tiếp xúc với (P)

Bài 14: Cho (P): $\displaystyle y=2{{x}^{2}}$

1. Vẽ (P)

2. Trên (P) lấy điểm A có hoành độ x = 1 và điểm B có hoành độ x = 2 . Xác định các giá trị của m và n để đường thẳng (d): y = mx + n tiếp xúc với (P) và song song với AB

Bài 15: Xác định giá trị của m để hai đường thẳng có Phương trình $\displaystyle \begin{array}{*{20}{c}} {({{d}_{1}}):x+y=m} \\ {({{d}_{2}}):mx+y=1} \end{array}$ cắt nhau tại một điểm trên (P) $\displaystyle y=-2{{x}^{2}}$ .

Cùng chuyên đề:

<< Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau khi rút gọnGiải và biện luận phương trình bậc nhất một ẩn >>

Đại số 9 - Tags: đồ thị hàm số, hàm số, hàm số bậc hai, hàm số bậc nhất, toán 9

Đồ thị hàm số bậc nhất và bậc hai

Dạng toán về Đồ thị hàm số bậc nhất y=ax + b và hàm số bậc hai y=ax^2 + b rất quan trọng trong chương trình ôn thi vào 10 môn Toán.

I. Điểm thuộc đường – đường đi qua điểm

II. Cách tìm giao điểm của hai đường y = f(x) và y = g(x)

III. Quan hệ giữa hai đường thẳng

IV. Tìm điều kiện để 3 đường thẳng đồng quy

V. Quan hệ giữa (d): y = ax + b và (P): y = ax² (a^’0)

1. Tìm tọa độ giao điểm của (d) và (P)

2. Tìm điều kiện để (d) và (P) cắt; tiếp xúc; không cắt nhau

VI. Viết Phương trình đường thẳng y = ax + b

VII. Chứng minh đường thẳng luôn đi qua 1 điểm cố định

VIII. Tìm khoảng cách giữa hai điểm bất kỳ A; B

IX. Một số ứng dụng của đồ thị hàm số

BÀI TẬP VỀ HÀM SỐ

Cách giải phương trình bậc cao – Bồi dưỡng Toán 9

Giải phương trình vô tỷ bằng phương pháp nâng lên lũy thừa

Cách rút gọn biểu thức chứa căn bậc hai – Toán 9

So sánh nghiệm của phương trình bậc 2 với một số

32 bài toán ôn tập thi học kì 1 Toán 9 phần Đại số

Tóm tắt kiến thức Toán 9 học kì 1: Đại số và Hình học

Công thức Toán 9 cần ghi nhớ: Đại số 9 và Hình học 9

Dạng toán về Đồ thị hàm số bậc nhất y=ax + b và hàm số bậc hai y=ax^2 + b rất quan trọng trong chương trình ôn thi vào 10 môn Toán.

I. Điểm thuộc đường – đường đi qua điểm

II. Cách tìm giao điểm của hai đường y = f(x) và y = g(x)

III. Quan hệ giữa hai đường thẳng

IV. Tìm điều kiện để 3 đường thẳng đồng quy

V. Quan hệ giữa (d): y = ax + b và (P): y = ax2 (a’0)

1. Tìm tọa độ giao điểm của (d) và (P)

2. Tìm điều kiện để (d) và (P) cắt; tiếp xúc; không cắt nhau

VI. Viết Phương trình đường thẳng y = ax + b

VII. Chứng minh đường thẳng luôn đi qua 1 điểm cố định

VIII. Tìm khoảng cách giữa hai điểm bất kỳ A; B

IX. Một số ứng dụng của đồ thị hàm số

BÀI TẬP VỀ HÀM SỐ

V. Quan hệ giữa (d): y = ax + b và (P): y = ax² (a^’0)