Giải và biện luận hệ phương trình bậc nhất hai ẩn
- Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
- Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau khi rút gọn
- Đồ thị hàm số bậc nhất và bậc hai
- Giải và biện luận phương trình bậc nhất một ẩn
- Giải và biện luận hệ phương trình bậc nhất hai ẩn
- Phương trình bậc hai – Hệ thức Vi-ét
- Cách tìm hai số khi biết tổng và tích của chúng
- Hệ phương trình đối xứng loại 1, loại 2 có hai ẩn
- Hệ phương trình bậc nhất chứa tham số
- Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
- Biện luận nghiệm của phương trình bậc 2 bằng đồ thị
- Các dạng bài tập giải bài toán bằng cách lập phương trình, hệ phương trình
- 30 bài tập hình học ôn thi vào 10 môn Toán
- Dạng bài tìm điều kiện về nghiệm của phương trình bậc hai
- Bài tập: Rút gọn biểu thức và câu hỏi phụ – Ôn thi vào 10
- Bài tập bất đẳng thức lớp 9 không chuyên
- 32 bài tập giải bài toán bằng cách lập phương trình, hệ phương trình cơ bản
- Các dạng bài tập Đại số ôn thi vào lớp 10
- Ôn thi vào 10 môn Toán năm học 2020-2021
- 5 đề thi thử vào lớp 10 THPT môn Toán năm 2021
- Đề thi thử môn Toán vào lớp 10 THPT năm 2021-2022 có lời giải
- Chuyên đề: Phương trình và hệ phương trình ôn thi vào 10
- 68 bài tập: giải toán bằng cách lập phương trình, hệ phương trình
- Một số bài hình ôn thi vào lớp 10 có lời giải
- Những bài toán hình học mẫu ôn thi HK2 và tuyển sinh vào 10 môn Toán
Giải và biện luận hệ phương trình bậc nhất hai ẩn nằm trong chuyên đề ôn thi vào 10 môn Toán.
Hệ Phương trình bậc nhất có hai ẩn số
+ Dạng tổng quát: ![]()
+ Cách giải:
- Phương pháp thế.
- Phương pháp cộng đại số.
+ Số nghiệm số:
- Nếu
 Thì hệ Phương trình có một nghiệm .
Thì hệ Phương trình có một nghiệm . - Nếu
 Thì hệ Phương trình có vô nghiệm .
Thì hệ Phương trình có vô nghiệm . - Nếu
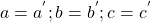 Thì hệ Phương trình có vô số nghiệm.
Thì hệ Phương trình có vô số nghiệm.
+ Tập nghiệm của mỗi Phương trình biểu diễn trên mặt phẳng toạ độ là đồ thị hàm số dạng: ![]()
Ví dụ: Giải các HPT sau:
Bài 1: ![]()
Giải:
+ Dùng PP thế:
![]()
![]()
HPT đã cho có nghiệm là: ![]()
+ Dùng PP cộng:
![]()
![]()
HPT đã cho có nghiệm là: ![]()
Bài 2: ![]() Để giải loại HPT này ta thường sử dụng PP cộng cho thuận lợi.
Để giải loại HPT này ta thường sử dụng PP cộng cho thuận lợi.
Giải:
![]()
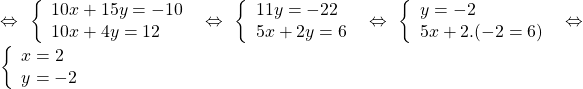
HPT có nghiệm là ![]()
Bài 3: 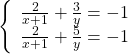
Giải:
* Đối với HPT ở dạng này ta có thể sử dụng hai cách giải sau đây:
+ Cách 1: Sử dụng PP cộng. ĐK: ![]() .
.
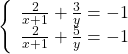
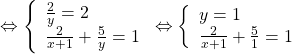
![]()
HPT có nghiệm là ![]()
+ Cách 2: Sử dụng PP đặt ẩn phụ. ĐK: ![]() .
.
Đặt ![]() ;
; ![]() . HPT đã cho trở thành:
. HPT đã cho trở thành:
![]()
![]() (TMĐK)
(TMĐK)
HPT có nghiệm là ![]()
Lưu ý:
– Nhiều em còn thiếu ĐK cho những HPT ở dạng này.
– Có thể thử lại nghiệm của HPT vừa giải.
Bài tập về hệ Phương trình
Bài 1: Giải các hệ phương trình sau (bằng pp thế)
a) ![]()
b) ![]()
c) ![]()
Bài 2: Giải các hệ phương trình sau (bằng pp cộng đại số)
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Bài 3: Giải hệ phương trình ![]() trong mỗi trường hợp sau
trong mỗi trường hợp sau
a) m = -1 b) m = 0 c) m = 1
Bài 4:
a) Xác định hệ số a và b, biết rằng hệ phương trình ![]() có nghiệm là (1; -2)
có nghiệm là (1; -2)
b) Cũng hỏi như vậy nếu hệ phương trình có nghiệm là ![]()
Bài 5: Giải hệ phương trình sau: ![]()
Từ đó suy ra nghiệm của hệ phương trình ![]()
Bài 6: Cho hệ Phương trình ![]()
a) Giải hệ khi a =3 ; b =-2
b) Tìm a;b để hệ có nghiệm là (x;y) = (![]()
Bài 7: Giải các hệ Phương trình sau: (pp đặt ẩn phụ)
a) 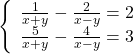
b) ![]()
c) ![]() (đk x;y
(đk x;y![]() 2 )
2 )
d) ![]() ;
;
e) ![]() ;
;
f) ![]() .
.
g) ![]() ;
;
h) ![]() ;
;
i) 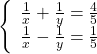 ;
;
k) 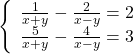 ;
;
l) 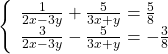 ;
;
Giải và biện luận phương trình bậc nhất một ẩn
Đồ thị hàm số bậc nhất và bậc hai
Cách giải phương trình bậc cao – Bồi dưỡng Toán 9
Giải phương trình vô tỷ bằng phương pháp nâng lên lũy thừa
Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
So sánh nghiệm của phương trình bậc 2 với một số
32 bài toán ôn tập thi học kì 1 Toán 9 phần Đại số
