Cách chứng minh bất đẳng thức bằng vectơ
- Lý thuyết cơ bản chứng minh bất đẳng thức
- Lời khuyên bổ ích khi học bất đẳng thức
- Phương pháp biến đổi tương đương chứng minh bất đẳng thức
- Ứng dụng bất đẳng thức để giải phương trình
- Một số bất đẳng thức phụ hay dùng
- Chọn điểm rơi trong bất đẳng thức như nào?
- Chứng minh bất đẳng thức bằng phương pháp đổi biến
- Bất đẳng thức Schur với t=1. Các kết quả hay sử dụng
- Sử dụng biểu thức phụ để tìm cực trị của biểu thức
- Chứng minh bất đẳng thức bằng phương pháp ghép cặp
- Ứng dụng Cosi ngược dấu chứng minh bất đẳng thức
- Cách chứng minh bất đẳng thức bằng vectơ
- Bất đẳng thức Côsi (Cauchy) và bài tập áp dụng
- Bất đẳng thức Bunhiacopxki và các kỹ thuật thường dùng
- Tuyển tập một số bài toán bất đẳng thức trong kì thi chuyên Toán 2020
- Bất đẳng thức Svac-xơ (bất đẳng thức cộng mẫu số)
Phương pháp chung để chứng minh bài toán bất đẳng thức bằng cách sử dụng vectơ mà các em được học từ lớp 10.
Ta có:
![]() với
với ![]()
và bởi ![]() , do đó:
, do đó:![]() .
.
Ứng dụng vectơ chứng minh bất đẳng thức
Bài toán 1: Cho ![]() ABC, CMR: cosA + cosB + cosC
ABC, CMR: cosA + cosB + cosC ![]() .
.
Giải
Thiết lập các vectơ đơn vị ![]() ,
, ![]() ,
, ![]() trên các cạnh AB, BC, AC của
trên các cạnh AB, BC, AC của ![]() ABC, ta được:
ABC, ta được:
![]()
![]()
![]()
Mặt khác ta luôn có:
![]()
![]()
![]() , đpcm.
, đpcm.
Bài toán 2: Cho ![]() ABC, CMR:
ABC, CMR: ![]() .
.
Giải
Gọi O là tâm đường tròn ngoại tiếp ![]() ABC, ta nhận được:
ABC, ta nhận được:
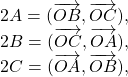
Mặt khác:
![]()
![]()
⇔ ![]() (đpcm)
(đpcm)
Bài toán 3: Chứng minh ![]() , ta có:
, ta có: ![]() (*)
(*)
Giải
Ta có (*) ![]()
![]()
Đặt:
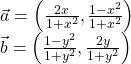
Suy ra : ![]()
Mà ![]() . Vậy
. Vậy ![]() (đpcm).
(đpcm).
Bài toán 4:
Cho ba số ![]()
![]()
![]() thỏa hệ thức
thỏa hệ thức ![]() Chứng minh rằng
Chứng minh rằng ![]()
Giải
Trong không gian với hệ tọa độ Đề-các vuông góc Oxy cho các vectơ :
![]()
![]()
Vì ![]()
![]()
![]()
Mặt khác ta có ![]() nếu
nếu ![]() nghĩa là
nghĩa là ![]() và
và ![]() cùng hướng. Vì
cùng hướng. Vì ![]() do đó
do đó ![]() nghĩa là
nghĩa là ![]() .
.
Do đó ta có:
![]()
Bài toán 5: Cho bốn số thực tùy ý ![]() . Chứng minh:
. Chứng minh:
![]()
Giải
Xét các vectơ:![]()
Áp dụng :![]()
![]()
![]()
Đẳng thức xảy ra khi ![]() cùng hướng
cùng hướng![]()
Bài toán 6: Cho 6 số thực a, b, c, d, x, y, z thỏa mãn: a + b + c = 2; ax + by + cz = 6
Chứng minh rằng:![]()
HD: Đặt ![]()
Bài tập
Bài 1: Cho ![]() ABC, CMR:
ABC, CMR: ![]() .
.
Bài 2: CMR:
a) ![]() .
.
b) ![]()
Bài 3: Tìm giá trị lớn nhất của biểu thức:![]()
Bài 4: Cho x, y, z là ba số dương và x + y + z ![]() 1
1
Chứng minh rằng: ![]()
Bài 5: (Đại học khối B 2006). Cho x,y là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức
![]()
Bài 6: Cho ba số thực x, y, z tùy ý. Chứng minh:
![]()
