Các bài toán sử dụng tỉ số diện tích hai tam giác – Toán lớp 5
- 30 chuyên đề bồi dưỡng HSG Toán lớp 5
- Dạng toán chuyển động của kim đồng hồ
- 168 bài toán lớp 5 chọn lọc có đáp án
- 76 bài tập hình học nâng cao lớp 5 có lời giải
- 27 bài toán nâng cao lớp 5 về số và chữ số
- 20 bài toán về mối quan hệ giữa bốn phép tính nâng cao lớp 5
- 14 bài toán về đại lượng tỉ lệ thuận, tỉ lệ nghịch nâng cao lớp 5
- 15 bài toán nâng cao lớp 5 về số thập phân
- 17 bài toán nâng cao lớp 5 giải bằng phương pháp giả thiết tạm
- 12 bài toán nâng cao lớp 5 giải bằng cách tính ngược từ cuối lên
- 22 bài toán chuyển động đều nâng cao lớp 5
- 10 bài toán nâng cao lớp 5 hay và khó
- Cách so sánh 2 phân số bất kỳ qua các ví dụ
- Một số bài toán về công việc chung nâng cao có lời giải
- 20 bài toán hình học nâng cao lớp 5
- Các bài toán sử dụng tỉ số diện tích hai tam giác – Toán lớp 5
- Các dạng bài toán về tính tuổi – Toán nâng cao lớp 5
- Bài tập tính giá trị biểu thức chứa phân số – Toán nâng cao lớp 4, 5
- Dạng toán về lịch, thời gian
- Các bài toán giải bằng biểu đồ Ven
- 100 câu hỏi trắc nghiệm tư duy Toán 5
- Một số bài toán về tỉ số và tỉ số phần trăm – Toán nâng cao lớp 5
- Dạng bài tập chữ số tận cùng của biểu thức
- Các dạng toán về dấu hiệu chia hết lớp 5
- Các bài toán về lịch thời gian có lời giải
- Các bài toán giải bằng phương pháp giả thiết tạm
- Các bài toán giải bằng phương pháp lựa chọn tình huống
- Các bài toán giải bằng phương pháp suy luận đơn giản
Sử dụng yếu tố tỉ số diện tích của hai tam giác là dạng toán thường gặp trong các đề thi vào lớp 6 ở các trường tổ chức thi tuyển.
Để làm được dạng bài tập toán nâng cao lớp 5 này, ngoài việc phải nhớ các công thức tính đường cao, diện tích của tam giác đã học các em cần nắm được hai điều sau:
– Hai tam giác có chung đáy thì tỉ số diện tích bằng tỉ số 2 đường cao tương ứng.
– Hai tam giác có chung đường cao thì tỉ số diện tích bằng tỉ số 2 đáy tương ứng.
Các em xem những ví dụ có lời giải dưới đây để hiểu rõ hơn về cách làm, từ đó áp dụng vào giải các bài tập tương tự.
Các ví dụ kèm lời giải:
Ví dụ 1: Cho tam giác ABC có diện tích 150cm2 . M là trung điểm của BC, N là trung điểm của AC. Nối MN. Tính diện tích tam giác CMN ?
Giải:
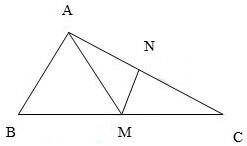
Ta có:
SABC = 2 x SAMC (chung chiều cao hạ từ A xuống đáy BC và đáy BC = 2 x MC)
Từ đó ta có: SAMC = 150 : 2 = 75 (cm2)
Ta có:SAMC = 2 x SCMN (chung chiều cao hạ từ M xuống đáy AC và đáy AC = 2 x NC)
Từ đó ta có: SCMN = 75 : 2 = 37,5 (cm2)
Đáp số: 37,5 cm2
Ví dụ 2: (Thi vào lớp 6 trường THCS chuyên Ngoại Ngữ 2019 – 2020)
Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF ?
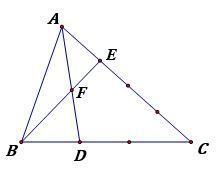
Giải:
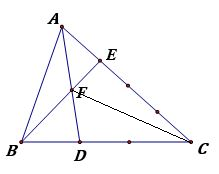
Ta có: ![]() nên
nên ![]()
Vậy ![]() (1)
(1)
Ta có: DC = 2 x BD nên ![]()
EC = 4 x AE nên ![]()
Vậy ![]() hay
hay ![]() (2)
(2)
Từ (1) và (2): ![]()
Vậy tỉ số là 2
Ví dụ 3: (Thi vào lớp 6 trường Hà Nội Amsterdam 2013 – 2014)
Cho hình chữ nhật ABCD, F là một điểm bất kì trên cạnh AD, BF cắt CD kéo dài tại điểm E. Nối điểm A với điểm E. Tính diện tích tam giác AEF, biết AF = 3cm, BC = 5cm, AB = 7 cm ?
Giải:
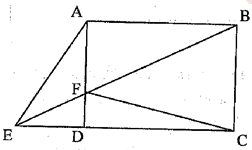
Ta có: ![]()
![]()
Suy ra diện tích tam giác AEF là:
![]()
Đáp số: 7 cm².
Ví dụ 4:(Thi vào lớp 6 trường Hà Nội Amsterdam 2011 – 2012)
Cho tam giác ABC biết BM = MC; CN = 3 x NA (như hình vẽ) và diện tích tam giác AEN bằng 27 cm².Tính diện tích tam giác ABC ?
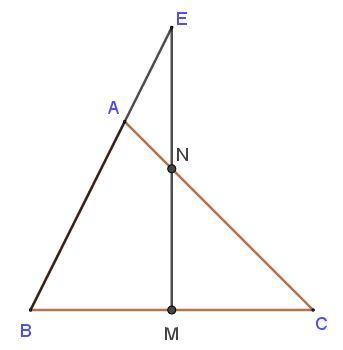
Giải:
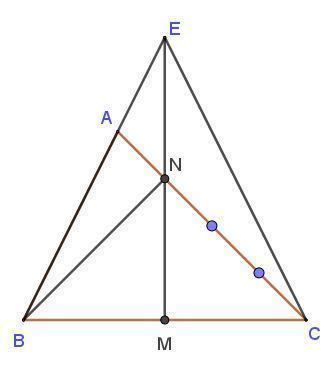
Nối E với C và B với N.
Ta có: CN = 3 x NA nên ![]()
Do BM = MC nên ![]() và
và ![]()
![]()
Diện tích tam giác ABC là:
54 x 4 = 216 (cm2 )
Đáp số: 216 cm2
Ví dụ 5:(Thi vào lớp 6 trường Archimedes Academy 2019 – 2020)
Cho hình vẽ bên biết ![]() . Tính
. Tính ![]()
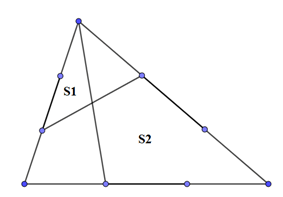
Giải:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Một số bài tập hình học nâng cao lớp 5
* Chú ý: Các bài tập dưới đây thường có trong đề thi tuyển sinh vào lớp 6 các trường THCS chuyên, chọn, chất lượng cao.
Bài 1: (Thi vào lớp 6 trường Archimedes Academy 2019 – 2020 – đợt 2)
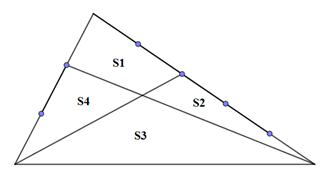
Cho tam giác với các tỷ lệ như hình.
Biết ![]() . Tính
. Tính ![]()
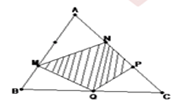
Bài 2: (Thi vào lớp 6 trường Hà Nội Amsterdam 2010 – 2011)
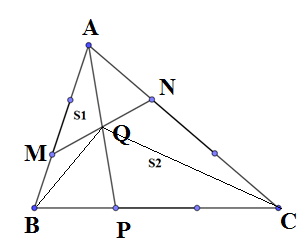
Cho tam giác ABC có diện tích là 180 cm2. Biết AB = 3 x BM; AN = NP=PC; QB=QC. Tính diện tích tam giác MNPQ ? (xem hình vẽ)
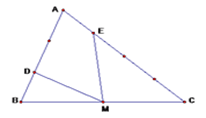
Bài 3: (Thi vào lớp 6 trường Hà Nội Amsterdam 2006 – 2007)
Cho tam giác ABC có diện tích bằng 18cm2. Biết DA = 2 x DB ; EC = 3 x EA ; MC = MB (hình vẽ). Tính tổng diện tích hai tam giác MDB và MCE ?
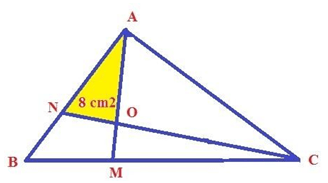
Bài 4: (Thi vào lớp 6 trường Hà Nội Amsterdam 2004 – 2005)
Trong hình vẽ bên có NA = 2 x NB; MC = 2 x MB và diện tích tam giác OAN là 8cm2. Tính diện tích BNOM ?
Bài 5:(Thi vào lớp 6 trường Hà Nội Amsterdam 2001 – 2002)
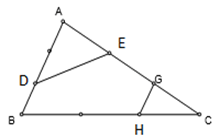
Cho tam giác ABC và các điểm D, E, G, H sao cho ![]() ;
; ![]() ;
; ![]() . Tính diện tích hình BDEGH ? ( Biết diện tích của tam giác ABC là 180cm2 )
. Tính diện tích hình BDEGH ? ( Biết diện tích của tam giác ABC là 180cm2 )
Cách giải bài toán hình tam giác lớp 5 cơ bản
Tính chu vi, diện tích hình tròn – Toán lớp 5
10 bài toán nâng cao lớp 5 hay và khó
22 bài toán chuyển động đều nâng cao lớp 5
Một số bài toán về tỉ số và tỉ số phần trăm – Toán nâng cao lớp 5
12 bài toán nâng cao lớp 5 giải bằng cách tính ngược từ cuối lên
17 bài toán nâng cao lớp 5 giải bằng phương pháp giả thiết tạm
