Các bài toán giải bằng biểu đồ Ven

Đây là bài thứ 20 of 28 trong chuyên đề Toán nâng cao lớp 5
Toán nâng cao lớp 5

Biểu đồ Ven (hay còn gọi là sơ đồ Ven) được sử dụng để giải các bài toán logic trong chương trình Toán nâng cao lớp 5.

Biểu đồ Ven có ý nghĩa như thế nào?

Biểu đồ Ven mô tả mối quan hệ giữa các đại lượng trong một bài toán.

Bài 1: Để phục vụ cho hội nghị quốc tế, ban tổ chức đã huy động 30 cán bộ phiên dịch tiếng Anh, 25 cán bộ phiên dịch tiếng Pháp, trong đó 12 cán bộ phiên dịch được cả 2 thứ tiếng Anh và Pháp. Hỏi:

a, Ban tổ chức đã huy động tất cả bao nhiêu cán bộ phiên dịch cho hội nghị đó.

b, Có bao nhiêu cán bộ chỉ dịch được tiếng Anh, chỉ dịch được tiếng Pháp?

Giải:

Số lượng cán bộ phiên dịch được ban tổ chức huy động cho hội nghị ta mô tả bằng sơ đồ ven.
Dạng toán giải bằng biểu đồ Ven


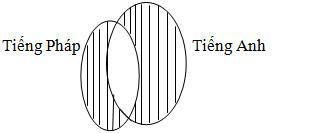
Nhìn vào sơ đồ ta có:

Số cán bộ chỉ phiên dịch được tiếng Anh là:

30 – 12 = 18 (người)

Số cán bộ chỉ phiên dịch được tiếng Pháp là:

25 – 12 = 13 (người)

Số cán bộ phiên dịch được ban tổ chức huy động là:

30 + 13 = 43 (người)

Đáp số: 43; 18; 13 người.

Bài 2: Lớp 9A có 30 em tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em nói được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu bạn nói được cả 2 thứ tiếng?

Giải:

Các em lớp 9A tham gia dạ hội được mô tả bằng sơ đồ ven.
Dạng toán giải bằng biểu đồ Ven


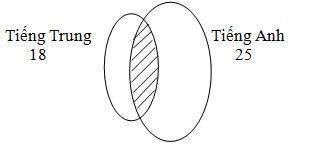
Số học sinh chỉ nói được tiếng Trung là:

30 – 25 = 5 (em)

Số học sinh chỉ nói được tiếng Anh là:

30 – 18 = 12 (em)

Số em nói được cả 2 thứ tiếng là:

30 – (5 + 12) = 13 (em)

Đáp số: 13 em.

Bài 3: Có 200 học sinh trường chuyên ngữ tham gia dạ hội tiếng Nga, Trung và Anh. Có 60 bạn chỉ nói được tiếng Anh, 80 bạn nói được tiếng Nga, 90 bạn nói được tiếng Trung. Có 20 bạn nói được 2 thứ tiếng Nga và Trung. Hỏi có bao nhiêu bạn nói được 3 thứ tiếng?

Giải:
Dạng toán giải bằng biểu đồ Ven


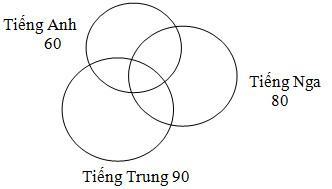
Số học sinh nói được tiếng Nga học tiếng Trung là:

200 – 60 = 140 (bạn)

Số học sinh nói được 2 thứ tiếng Nga và Trung là:

(90 + 80) – 140 = 30 (bạn)

Số học sinh nói được cả 3 thứ tiếng là:

30 – 20 = 10 (bạn)

Đáp số: 10 bạn.

Bài 4: Trong 1 hội nghị có 100 đại biểu tham dự, mỗi đại biểu nói được một hoặc hai trong ba thứ tiếng: Nga, Anh hoặc Pháp. Có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?

Giải:
Dạng toán giải bằng biểu đồ Ven
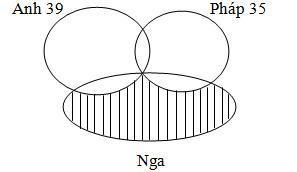
Số đại biểu nói được tiếng Pháp hoặc Nga là:

100 – 39 = 61 (đại biểu)

Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Pháp là:

61 – 35 = 26 (đại biểu)

Số đại biểu chỉ nói được tiếng Nga là:

26 – 8 = 18 (đại biểu)

Đáp số: 18 đại biểu.

Bài tập tự giải

Bài 1: Lớp 5A có 15 ban đăng kí học ngoại khoá môn Văn, 12 bạn đăng kí học ngoại khoá môn Toán, trong đó có 7 bạn đăng kí học cả Văn và Toán. Hỏi:

a, Có bao nhiêu bạn đăng kí học Văn hoặc Toán?

b, Có bao nhiêu bạn chỉ đăng kí học Văn? chỉ đăng kí học Toán?

Bài 2: Trên 1 hội nghị các đại biểu sử dụng một hoặc hai trong 3 thứ tiếng: Nga, Anh hoặc Pháp. Có 30 đại biểu nói được tiếng Pháp, 35 đại biểu chỉ nói được tiếng Anh, 20 đại biểu chỉ nói được tiếng Nga và 15 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi hội nghị đó có bao nhiêu đại biểu tham dự?

Bài 3: Bốn mươi em học sinh của trường X dự thi 3 môn: ném tạ, chạy và đá cầu. Trong đội có 8 em chỉ thi ném tạ, 20 em thi chạy và 18 em thi đá cầu. Hỏi có bao nhiêu em vừa thi chạy vừa thi đá cầu?

Bài 4: Đội tuyển thi học sinh giỏi của tỉnh X có 25 em thi Văn và 27 em thi toán, trong đó có 18 em vừa thi Văn vừa thi toán. Hỏi đội tuyển học sinh giỏi 2 môn Văn và Toán của tỉnh X có bao nhiêu em?

Cùng chuyên đề:

<< Dạng toán về lịch, thời gian100 câu hỏi trắc nghiệm tư duy Toán 5 >>

Toán lớp 5 - Tags: , , ,